Although many people charged with developing data acquisition (DAQ) systems are professional test engineers, most are not. For those without formal training and years of experience in the DAQ world, selecting the most appropriate system can be a daunting task. In particular, DAQ interfaces have a large number of specifications that must be considered when selecting the best system for a particular application.
While DAQ systems include many different functions and capabilities, the analog input is of prime importance for the vast majority of applications. Measuring temperature, pressure, strain, vibration, current, or even a simple voltage requires an analog input with a wide variety of specifications.
Number of Channels
Probably the easiest and most obvious specification to consider is the number of channels the system requires. The system must have at least as many inputs as you have signals you wish to measure.
However, there are a couple of potential gotchas to consider as well. The first is whether the interface has both differential and single-ended inputs. If it has both, the number of channels specified in the product description, such as 16-channel 16-b A/D board, will almost always be the number of single-ended channels. The number of differential channels will be half that. Nobody is trying to trick you. It�s just the convention on which the industry has standardized.
Another item to consider is whether your system has any hidden analog input requirements. For example, if you are using a sensor that is very sensitive to ambient temperature and will be deployed in an outdoor environment, to make an accurate measurement, it might be necessary to measure the temperature at the sensor as well. When measuring temperature from thermocouples (TCs), at least one input channel will likely be required for cold junction compensation.
Resolution
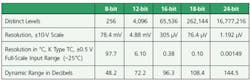
The resolution of an analog input channel describes the number or range of measurement values the system can provide. This specification is almost universally listed in terms of bits, where the resolution is defined as 2(# of bits). For example, 8-b resolution corresponds to a resolution of one part in 28 or 256.
When combined with an input range, the resolution determines how small a change in the input is detectable. To establish the resolution in engineering units, divide the range of the input by the resolution. The actual equation requires the input range be divided by 2(# of bits) -1; however, for resolutions greater than 10 b, the error typically is negligible for purposes of specifying system performance. A 16-b input with a 0 to 10-V input range provides 10 V/216 or 152.6 �V.
Eight-bit converters commonly are used in extremely high-speed applications while 20-b and 24-b converters are becoming common in applications that require more resolution but at lower sample rates. Table 1 provides a comparison of the resolutions for the most commonly used converters in DAQ systems.
Table 1. Resolution and Dynamic Range for Commonly Used DAQ Devices
Dynamic range is another factor to consider regarding resolution. It is the ratio between the minimum resolution and the input�s full scale. Though dynamic range is not a key specification in many applications, when monitoring a signal normally plotted on a log scale, dynamic range is an important consideration.
Acoustics and vibration and seismology are two applications where dynamic range is of critical importance. The advent of inexpensive 24-b A/D converters has increased the capability to accurately and cost-effectively monitor these signals.
Accuracy
Although accuracy often is equated with resolution, they are not the same specification. Just because an analog input system can resolve a 1-�V signal, it does not mean the input is accurate to 1 �V. It is possible a system with 1-�V resolution might only provide a signal accurate to 1 mV.
For example, a 24-b A/D converter with an input range of 0 to 10 V has
0.596-�V resolution. But, it might only provide DC accuracy of 1 mV. It�s not uncommon for 24-b A/D converters for audio systems to have gain/full-scale error on the order of 2%.
In voltage terms, assuming our 0 to 10-V input range, resolution is 0.596 �V, but the DC accuracy might be as low as 20 mV. The 20-mV accuracy is perfectly adequate for the audio application but not likely good enough for a temperature or pressure measurement. Of course, this is an extreme case and, although absolute accuracy is not always a critical issue, it is in many applications. Remember that high resolution does not always ensure high accuracy.
While resolution is almost uniformly specified in bits, accuracy specifications are offered in a wide assortment of terminology. No one way is correct, and depending on the application, one specification method might provide more insight than another.
The primary error contributors of an analog input system are input offset, gain error, nonlinearity, and inherent system noise. Combine offset, gain, and integral nonlinearity (INL) with the input noise specification to calculate the overall input accuracy.
There are additional secondary contributing factors, but for most applications and in most systems, they can be ignored. Figure 1 shows the relationship between a perfect input system and how each of the errors impacts the measurement.
Figure 1. Graphical Representation of Offset, Gain, and INL Errors
Input Offset
Assuming all other errors are zero, input offset is a constant difference between the measured input and the actual input voltage. For example, if the input offset voltage was +0.1 V, measurements of perfect 1-, 2-, and 5-V input signals would provide readings of 1.1, 2.1, and 5.1 V, respectively.
In a real system, the other three errors are never zero, which complicates the measurement of input offset. For this reason, most specifications define the input offset as the measurement error at 0 V.
Some DAQ products, such as the DNA-AI-207 Analog Input Board in Figure 2, provide an auto-zeroing capa-
bility. This function drives the input offset error to zero or at least to a level small enough that its contribution is no longer significant relative to other errors.
Figure 2. PowerDNA DAQ With DNA-AI-207 Analog Input Board
Gain Error
Once again, we�ll explain this error by first assuming all other errors are zero. In this case, gain error is the difference in the slope in volts per bit between the actual system and an ideal system. For example, if the gain error is 1%, the gain error at 1 V would be 10 mV while the error at 10 V would be 10 times as large at 100 mV.
In a real-world system where the other errors are not zero, the gain error usually is defined as the error of the measurement at the full-scale reading. For example, in our 0 to 10-V example range, if the error at 10 V or more often at a reading arbitrarily close to 10 V such as 9.9 V is 1 mV, the gain error specified would be 100x(0.001/10) or 0.01%. For higher precision measurement systems, the gain error often is specified in parts per million (ppm) rather than percent since it�s a bit easier to read.
To calculate the error in ppm, multiply the input error divided by the input range by one million. In our example, the 0.01% would be equivalent to 1,000,000x(0.001/10) or 100 ppm.
Although many products offer auto-calibration that reduces the gain error, unlike the input offset error, it is not possible to eliminate it completely. This is because the automated gain calibration is performed relative to an internally supplied reference voltage.
The reference voltage will have its own error, and any error in the reference translates into a gain error. As the gain error gets small relative to other system errors, it becomes uneconomical to improve the reference accuracy.
Nonlinearity
As its name implies, nonlinearity is the difference between the plot of the input measurement vs. the actual voltage and the ideal measurement�s straight line. The nonlinearity error is provided in two components: INL and differential nonlinearity (DNL).
INL, the specification of importance in most DAQ systems, typically is provided in bits, and it describes the maximum error contribution due to the deviation of the voltage vs. the reading curve from a straight line. Although a somewhat difficult concept to describe, INL is easily depicted in Figure 1.
DNL describes the jitter between the input voltage change required for the A/D converter to increase or decrease by one bit. In an ideal converter, the voltage increase to go from one reading to the next higher is identical and exactly equal to the system resolution.
For example, in a 16-b system with a 10-V input range, the resolution per bit is 152.6 �V. An ideal converter would increase its digital output by one bit each time the input voltage increased by 152.6 �V. However, A/D converters are not ideal, and the voltage increment required to move to the next higher bit is not a fixed amount.
DNL typically should be �1 LSB or less. A DNL specification greater than �1 LSB indicates missing codes are possible. Though not as problematic as a nonmonotonic D/A converter, A/D missing codes do compromise measurement accuracy.
Noise
Noise is an ever-present error in all DAQ systems. Much of the noise in any system is generated by the external system and pick-up in the cabling. However, every DAQ system has inherent noise as well. Typically, this noise is measured by shorting the inputs at the board or device connector and acquiring a series of samples.
An ideal system response would be a constant zero. However, in almost all systems, the reading will bounce around over a number of samples. The magnitude of the bounce is the inherent noise. The noise specification can be provided in either bits or volts and as peak-to-peak or rms.
Noise must be factored into the overall error calculations. Note that a 16-b
input system with 3-b rms of noise is not going to provide much better than 13-b accuracy as the 3 LSB will be dominated by noise and contain very little useful information.
Put It All Together
Although it is unlikely that all three of the offset, linearity, and gain errors will contribute in the same direction, it is certainly risky to assume they will not. It is seldom prudent to ignore Murphy�s law.
Maximum Sample Rate
The system must sample fast enough to be able to see the required changes in input. Without going into details on Nyquist sampling theory, it is probably sufficient to say you must sample at least twice as fast as the phenomenon you wish to monitor is changing. If your input signal contains frequencies up to 1 kHz, you will want to sample at 2 kHz and more realistically at 3 kHz.
Be careful to examine the analog input systems you are considering to know whether the sample-rate specification is for each channel or for the entire board. Most manufacturers specify sample rate as applicable for the entire board. For a 100-kS/s sample rate, one channel is sampled at the maximum rate but additional channels must share the 100 kS/s.
For example, if two channels are sampled, each may only be sampled at 50 kS/s. Similarly, five channels could be sampled at 20 kS/s each. If the sample rate is not specified as per-channel, the rate must be divided among the channels sampled.
Another sample-rate consideration is required when the DAQ system is monitoring inputs with widely varying frequency content. For example, an automotive test system may need to monitor vibration at 20 kS/s and temperature at 1 S/s. If the analog input only samples at a single rate, the system will be forced to sample temperature at 20 kS/s and waste a great deal of memory with the 19,999 temperature S/s that aren�t needed. Some systems allow each channel to be sampled at a different rate while many do not.
The final concern is the need to sample fast enough or provide filtering to prevent aliasing. If signals included in the input signal are at higher frequencies than half the sample rate, there is the risk of aliasing errors. Without going into the mathematics of aliasing, we will just say that these higher frequency signals can and will manifest themselves as a low-frequency error.
A real-life example of aliasing is common in movies. The spokes of a wheel appearing to move slowly or backwards is an example of aliasing. In the movies it doesn�t matter, but if the same phenomenon appears in the measured input signal, it�s a pure and sometimes critical error.
There really are two solutions for aliasing. The first and often simplest is to sample at a rate higher than twice the highest frequency component in the signal measured. Some measurement purists will say that you can never be sure what the highest frequency in a signal will be. But in reality, many systems designers have very good a priori knowledge of the frequencies included in a given input signal.
People do not use anti-aliasing filters on thermocouples because they are almost never needed. With a good idea of the basics of the signals measured, it usually is a straightforward decision to determine if aliasing might be a problem or not.
In some applications such as audio and vibration analysis, aliasing is a very real concern, and it is difficult to guarantee that a sample rate is faster than every frequency component in the waveform. These applications require an anti-aliasing filter. These typically are 4-pole or greater filters set at one-half the sample rate. They prevent the higher-frequency signals from getting to the system A/D converter where they can create aliasing errors.
Input Range
Though a fairly obvious specification, input range is not one to ignore. If you have a �15-V signal, you�re not going to be happy with the results from a DAQ board with a fixed �5-V input range. Most systems these days have software-programmable input ranges. Either way, the signal measured should be smaller than the maximum input range of the DAQ input device.
One other input range consideration is whether the DAQ device is capable of setting different channels at different ranges. A single input range system measuring diverse signals such as a thermocouple and a �10-V input will require the system be set at a gain low enough to cover the input with the largest full-scale range. This, in effect, reduces the resolution available on signals with smaller, full-scale input ranges.
Differential vs. Single-Ended
A differential input measures the voltage difference between two input terminals while a single-ended input reads the difference between an input and the DAQ ground. Differential inputs offer better noise immunity for two reasons.
First, much of the noise in a DAQ system is picked up when EMI in the local environment is coupled into system cables. Keeping the two wires in a differential input in close proximity means both wires are subject to the same EMI. Since the EMI pickup will be identical on both wires, it does not show up as a difference in voltage at the two inputs and does not impact the measurement.
Differential signals also can float within a range referred to as the common-mode range relative to ground. A slight difference in the voltage of the ground at the DAQ system and at the sensor or signal source is largely ignored by differential inputs but creates a tug of war that can move the DAQ system ground around enough to cause significant single-ended measurement error.
The noisier the environment, the more important it is to have differential inputs. At 16-b resolution or higher, it usually is recommended to use differential inputs. Most vendors do not offer interfaces with higher than 16-b resolution in the single-ended mode because the noise picked up by the high-resolution, single-ended input is almost certain to disappoint the customer.
Sampling Mode
Most multichannel DAQ boards are based on a single A/D converter. A type of switch called a multiplexer is used between the input channels and the A/D converter. The multiplexer connects a particular input to the A/D, allowing it to sample that channel. The multiplexer then switches to the next channel in the sequence, and another sample is taken. This goes on until all the desired channels have been sampled.
This configuration provides inexpensive, yet accurate, measurements. But even if switching and sampling are very fast, the samples actually are taken at different times.
In most applications, the time skew between samples on different channels is not problematic. In some high-speed applications, these skews or phase shifts between signals cannot be tolerated, and a standard multiplexed system cannot be used.
In this case, the system requires the capability to sample different channels simultaneously, which can be accomplished in two ways. The first is to place a sample and hold (S&H) on each multiplexer input. When commanded to hold, the S&H effectively freezes the input at that instant on its output.
In hold mode, even as the input changes, the output remains constant. Once in hold mode, the multiplexed A/D system samples the desired channels, and the data it provides will have come from samples taken at the same time.
The second way requires an independent A/D converter on each channel. Either system should provide good results.
Conclusion
Since an in-depth discussion of specifications is quite involved, we have focused only on the key issues. However, should you have any trouble interpreting a particular DAQ vendor�s specification, contact the company and ask for help. Not only is it the simplest way to get the information you require, it also is a great opportunity to evaluate the company�s commitment to customer service and technical support.
About the Author
Bob Judd is director of marketing at United Electronic Industries. Prior to joining UEI, he was general manager and vice president of marketing and hardware engineering at Measurement Computing and previously vice president of marketing at MetraByte. Mr. Judd holds a bachelor�s degree in engineering from Brown University and a master�s degree in management from MIT. United Electronic Industries, 611 Neponset St., Canton, MA 02021, 781-713-0023, e-mail: [email protected]
FOR MORE INFORMATION
on simultaneous sampling
analog input layers
www.rsleads.com/707ee-194
July 2007