Electronicdesign 29225 Promo Ifdvol1 No4 0

Synthesized Inductor Delivers Maximum Power Transfer

July 19, 2012

To transfer maximum power within a circuit, the load resistance must match the source resistance. In the case of a complex load, this can be done by substituting a synthesized inductor for a bulky physical inductor.

Michael Gambuzza

>> Electronic Design Resources
.. >> Library: Article Series
.. .. >> Series: Ideas for Design
.. .. .. >> Ideas for Design Vol. 1

Download this article as a PDF file

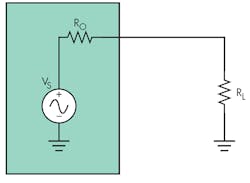
To transfer maximum power from a circuit to a load, the load’s resistance, R_L, must match the source resistance, R_o (Fig. 1). In the case of a complex load, Z_L, and a resistive source, this transfer can require the use of a bulky inductor. This idea shows how to replace the physical inductor with a smaller synthesized inductor.

Electronicdesign Com Sites Electronicdesign com Files Ifd2 Fig1

1. The simplest matching circuit consists of a resistive load, R_L, equal to the source resistance, R_o.

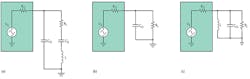
A good example of a complex load is a piezoelectric transducer represented by the Butterworth-Van Dyke model as C_o, R_L, C_s, and L (Fig. 2a). At series resonance, the load impedance reduces to the equivalent circuit shown in Figure 2b. The load is still complex, with R_L in parallel with C_o. This makes matching to R_o impossible without a complex conjugate match of –C_o at the source—that is, an inductor in parallel with C_o and having the same magnitude of reactance (Fig. 2c).

Electronicdesign Com Sites Electronicdesign com Files Ifd2 Fig2

2. An example of a complex load is a Butterworth-Van Dyke model of a piezoelectric transducer (a), which can be reduced to an equivalent circuit (b). To match the load to the source, an appropriate inductor, L, must be added (c).

To match R_o to R_L, L must be chosen to “resonate out” C_o:

–XC_o = X_L

– {–j[1/(ωC_o)]} = jωL

Therefore:

L = 1/(ω² × C_o)

where:

ω = 2πf

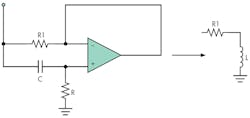
To replace the physical inductor, L, with a synthesized inductor, consider the gyrator circuit, which Bernard Tellegen invented in 1948 (Fig. 3). The circuit is basically a differentiator in which the operation of capacitor C is reversed. The simulated inductance becomes:

L = (R1)(R)(C) Henries

Electronicdesign Com Sites Electronicdesign com Files Ifd2 Fig3

3. Instead of a bulky physical inductor, the designer can use this gyrator circuit, which provides a simulated inductance equal to (R1)(R)(C).

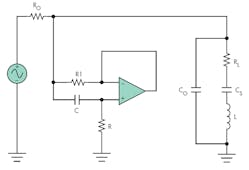
Typically, R1 is kept to 100 Ω or less so the circuit’s Q can be at least 10. (Details of the gyrator circuit are available on the Internet. For example, see www.beigebag.com/case_gyrator.htm. Figure 4 shows the final implementation of the matched circuit. With this circuit, R can be dynamically varied to change the tuning on the fly for different complex loads, provided that the voltage across the load is measured so optimum tuning can be achieved.

Electronicdesign Com Sites Electronicdesign com Files Ifd2 Fig4

4. In a typical implementation of the gyrator matching circuit, dynamically varying R can change the tuning of the circuit for different complex loads, provided that the voltage across the load is measured to ensure optimum tuning.

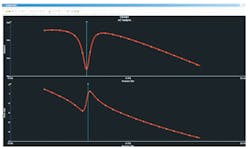
Figure 5 shows the simulation results of a tuned circuit using the described gyrator circuit. The top trace is the voltage across the load, which shows a minima at the resonant frequency. The bottom trace shows the phase of the voltage across the load, which is 0° at resonance. These results indicate that the selected synthesized inductance successfully matches the load to the source.

Electronicdesign Com Sites Electronicdesign com Files Ifd2 Fig5

5. In these simulation results, the voltage across the load (top trace) shows a minima at the resonant frequency. The phase of the voltage across the load (bottom trace) is 0° at resonance. These results indicate the selected inductance created a successful match.