A three-point-delta method provides more accurate resistance measurements in low-voltage applications.
Electronic components are continuing to shrink as consumers demand faster, more feature-rich products in ever-smaller form factors. Because of their small sizes, these electronic components usually have limited power-handling capability. As a result, when electrically characterizing these components, the test signals need to be kept small to prevent breakdown or other damage.
Testing these devices and materials often includes making low-voltage measurements. This involves sourcing a known current, measuring the resulting voltage, and calculating the resistance. If the device has a low resistance, the resulting voltage will be very small, and great care needs to be taken to reduce offset voltage and noise.
Even if the resistance is far from zero, the voltage to be measured often is very small because only a small current can be sourced to avoid damaging the device. This power limitation often makes characterizing the resistance of modern devices and materials very challenging.
Low-Level Voltage Measurements
Many factors make low-voltage measurements difficult. For instance, various noise sources can prevent resolving the actual voltage, and thermoelectric voltages (thermoelectric EMFs) can cause error offsets and drift in voltage readings.
In the past, it would have been possible to simply increase the test current until the device�s response voltage was much larger than the errors. But with today�s smaller devices, this is no longer an option. Increased test current can cause heating, which eventually could destroy the device.
The key to obtaining accurate, consistent measurements is eliminating the error. For low-voltage measurement applications, such error is composed largely of white noise and 1/f noise. Thermoelectric voltages typically having 1/f distribution are generated from temperature differences in the circuit.
Resistance is calculated using Ohm�s Law; that is, the DC voltage measured across the device divided by the DC stimulus current yields the resistance. The voltage readings will be a sum of the induced voltage across the device (VR), lead and contact resistance (Vlead res), other 1/f noise contributions (V1/f noise), white noise (Vwhite noise), and thermoelectric voltages (Vt).
Using four separate leads to connect the voltmeter and current source to the device eliminates lead resistance because the voltmeter doesn�t measure the voltage drop across the source leads. Implementing filtering may reduce white noise but will not reduce 1/f noise significantly, which often sets the measurement noise floor.
Thermoelectric voltages normally have a 1/f characteristic. This means there can be significant offset, and the more measurements that are made the more drift. Taken together, the offset and drift may even exceed VR�the voltage across the device induced by the applied current. It�s possible to reduce thermoelectric voltages using techniques such as all-copper circuit construction, thermal isolation, precise temperature control, and frequent contact cleaning.
No matter what steps are taken to minimize thermoelectric voltages, it�s impossible to eliminate them. A method that would allow accurate resistance measurements even in the presence of large thermoelectric voltages is preferable instead of trying to minimize them.
Delta Method of Measuring Resistance
One way to eliminate a constant thermoelectric voltage is to use a delta method where voltage measurements are made first at a positive and then at a negative test current. A modified technique can be used to compensate for changing thermoelectric voltages.
Over the short term, thermoelectric drift can be approximated as a linear function. The difference between consecutive voltage readings is the slope or rate of change in thermoelectric voltage. This slope is constant, so it can be canceled by alternating the current source three times to make two delta measurements: one at a negative-going step and one at a positive-going step.
For the linear approximation to be valid, the current source must alternate quickly, and the voltmeter must make accurate measurements within a short period of time. If these conditions are met, the three-step delta technique provides an accurate voltage reading of the intended signal unaffected by thermoelectric offsets and drifts.
An analysis of the mathematics for one three-step delta cycle will demonstrate how the technique compensates for temperature differences in the circuit, reducing measurement error.
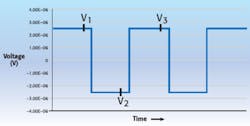
Figure 1a shows a series of measurements made as the test current is alternately applied in the forward and reverse directions. No thermal effects are present.
The exact measurement times are not shown but are identical relative to the start of each positive or negative segment. This means that the time between any two successive measurements is the same. The measurement results are referred to as V1, V2, and V3; in this ideal case, +2.5 �V, -2.5 �V, and +2.5 �V, respectively.
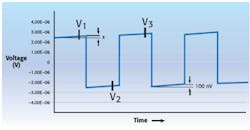
In Figure 1b, a positive thermal drift adds an offset of 100 nV each measurement interval. As in the case of zero thermal drift, we don�t know exactly when the measurements are made, but we do know that each successive measurement is offset by 100 nV from the previous measurement. Va and Vb are defined as the delta voltages.
The difference between the first two measurements is reduced by the positive thermal drift:
Va = (V1 – V2)/2
= (+ 2.5 + X – (- 2.5 + X + 0.1))/2
= 2.45 �V
where: X = unknown amount by which
V1 is offset due to thermal drift
Similarly, the difference between the second pair of measurements is affected by the thermal drift:
Vb = (V3 – V2)/2
= (+ 2.5 + X + 0.2 – (- 2.5 + X + 0.1))/2
= 2.55 �V
The final voltage is the average of the two delta voltages:
Vf = (Va + Vb)/2 = 2.5 �V
The delta technique eliminates error due to changing thermoelectric voltages. As a result, the measurement is the voltage induced by the stimulus current alone. As alternation continues, every successive reading is the average of the three most recent A/D conversions.
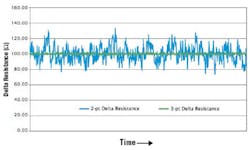
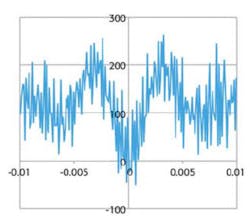
The three-step delta technique is the best choice for high-accuracy re-sistance measurements. Figure 2? resistor made with a 10-nA test current taken over approximately 100 s. In this example, the rate of change in thermoelectric voltage is no more than 7 �V/s. compares 1,000 measurements of a 100-
As shown, the two-step delta technique fluctuates 30% as the thermoelectric error voltage drifts. In contrast, the three-step delta technique has much lower noise�the measurement is unaffected by the thermoelectric variations in the test circuit.
Equipment Requirements
The success of the three-step delta method depends on the linear approximation of the thermal drift viewed over a short time period. This approximation requires that the measurement cycle time be faster than the thermal time constant of the test system. This imposes certain requirements on the current source and voltmeter.
The current source must alternate quickly in evenly timed intervals so the thermoelectric voltage changes an equal amount between each measurement. The voltmeter must be tightly synchronized with the current source and capable of making accurate measurements rapidly. The instruments must be synchronized so the voltmeter makes voltage measurements only after the current source has settled, and the current source doesn�t switch polarity until after the voltage measurement has been completed.
The measurement speed of the voltmeter is critical in determining total cycle time; faster voltage measurements mean shorter cycle times. For reliable resistance measurements, the voltmeter must maintain speed without sacrificing low-noise characteristics.
In low-power applications, the current source must be capable of outputting low values of current so as not to exceed the maximum power rating of the device. This capability is particularly important for moderately high- and high-impedance devices.
Differential Conductance
Another important measurement technique for characterizing solid-state and nanoscale devices is differential conductance. This technique is rarely simplified to Ohm�s Law.
For nonlinear devices, the resistance is no longer a constant, so a detailed measurement of the slope of the IV curve at every point is needed. The derivative is called the differential conductance
dG = dI/dV
or its inverse, the differential resistance
dR = dV/dI
The fundamental reason that differential conductance is interesting is that the conductance reaches a maximum at voltages at which the electrons are most active. In different fields, this measurement may be called electron-energy spectroscopy, tunneling spectroscopy, or density of states.
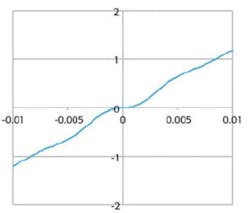
Typically, researchers perform differential conductance measurements using one of two methods: obtaining an I-V curve with a calculated derivative or using an AC technique. The I-V curve method requires only one source and one measurement instrument, which makes it relatively easy to coordinate and control.
A current-voltage sweep is made and the mathematical derivative is determined (Figure 3a and 3b). However, taking the mathematical derivative amplifies any measurement noise, so tests must be run multiple times and the results averaged to smooth the curve before the derivative is calculated. This leads to long test times.
The AC technique reduces noise and test times. It superimposes a low-amplitude AC sine wave on a swept DC bias. This involves many pieces of equipment and is hard to control and coordinate.
There is, however, another way to obtain differential conductance measurements that is both simple and low noise. This technique involves a current source that combines the DC and AC components into one instrument. There is no need to do a secondary measure of the current because the instrument is a true current source.
The resulting waveform can be broken down into an alternating current and a staircase current. Using the exact same calculations as in the delta method, accurate resistance or conductance measurements can be made at each point of the staircase. Because the three-step delta technique eliminates linearly drifting offsets, it also is immune to the effects of the linearly changing staircase.
There are several benefits for this method. In the areas of highest conductance, more data points are taken by sourcing the sweep in equal current steps. In addition, having just one instrument that both sources current and measures voltage simplifies equipment setup. Lastly, the reduced noise can lower test times from approximately an hour to only five minutes.
Conclusion
Thermoelectric EMFs often are the dominant source of error in low-resistance measurements. This error may be removed almost completely using a three-point current reversal technique. It�s no longer necessary to take extreme care to minimize thermally induced voltage noise in the wiring of resistance measuring systems. Applying the same technique to differential conductance measurements reduces noise and test complexity.
About the Author
Adam Daire is a product line manager at Keithley Instruments. Prior to this position, he spent nine years in product development for Keithley before moving to strategic marketing. Mr. Daire holds a B.S. in physics from Case Western Reserve University and an M.B.A. from the Weather-head School of Management. Keithley Instruments, 28775 Aurora Rd., Cleveland, OH 44139, 440-498-2853, e-mail: [email protected]
June 2005