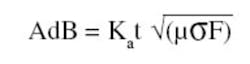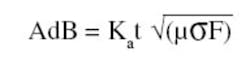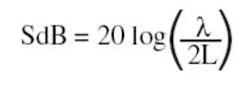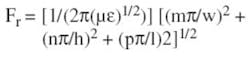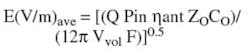Some older engineers actually took a course in mechanical drafting that used triangles, T-squares, and holders with different grades of lead (graphite). Sketching 3-D drawings of boxes, cylinders, machinery, electric motors, and components was particularly challenging. That�s when the class learned about vanishing points, the visual point where parallel lines converge and disappear. A good example is the highway that appears to become narrower as the distance increases.
A similar thing is happening to shielded enclosures. If we examined the continuum from the early days of radio until today, we would find that RF chambers with simple metal-lined walls became RFI shielded rooms with RF gaskets around any movable panels that became today�s precision EMC shielded enclosures, cabinets, and boxes.
Simultaneously, the RF frequencies kept increasing into the microwave region with smaller and smaller wavelengths while the components were decreasing in size and weight. Now, many of the final products are being carried in people�s purses and pockets or clipped onto their ears.
The RF gasket industry has done a reasonable job of keeping up with the shrinking enclosures. But as far as the miniature microwave PCB shielded enclosures are concerned, RF gaskets have almost reached the vanishing point. They are rapidly being replaced by direct solder connections to the PCB.
It�s not that gaskets are unable to provide sufficient attenuation. When combined with good PCB design, most of them permit equipment/systems to meet the commercial EMC requirements. Many of them also comply with the more stringent military requirements.
All of these gaskets, however, have one thing in common: There is a physical limitation on how small they can be economically manufactured.
This is significant because many of the new hand-held devices on the market today have PCB-mounted shielded boxes so small they cannot accommodate even the smallest of these gaskets. When the requirement is small, smaller, and smallest, the most cost-effective solution is a small metal PCB enclosure soldered in place. However, this is not a retro-fix. It must be designed in from the beginning.
Regardless of their small size, most electronic devices must comply with governmental EMC requirements, and many use shielding. Shielding is the only noninvasive suppression technique available, and it can reduce both radiated emissions and susceptibility.
There are, however, several points that must be considered:
� The PCB shielded enclosure should completely�and only�contain the circuit that is being protected. This may mean that multiple postage stamp-sized enclosures are required or that the enclosure is baffled and compartmentalized. Smaller is better.
� In a multilayer PCB, the shielded enclosure typically uses a PCB ground plane as one side of the shield. Accordingly, the separation distance from the surface of the enclosure to any surface components and traces will determine the capacitive coupling to the enclosure and ground. At microwave frequencies, this must be considered.
� The size of the enclosure must be small with respect to the operating frequency. Enclosure resonance occurs once the longest dimension of the enclosure reaches one-half wavelength or greater. Ideally, the longest dimension should be less than ?/6.
� Enclosures used to protect circuits for both radiated emissions and susceptibility should be designed with maximum absorption loss. Absorption loss can be enhanced using absorber materials inside the enclosure.
� Permeable materials should be used for low-impedance magnetic fields.
� Discontinuities should be kept to a minimum and designed to maintain shielding effectiveness. Connectors are considered discontinuities.
The maximum shielding effectiveness of an enclosure is determined by the properties of the enclosure materials and the incident RF wave impedance. All other design characteristics such as seams, apertures, and penetrations reduce the overall shielding effectiveness.
The two principal loss mechanisms are the energy reflection from the surface of the enclosure and the absorption within the enclosure material. If the RF source is located external to the shield, then the reflected RF energy propagates away from the enclosure and adds to the shielding effectiveness.
The enclosure design to reduce radiated susceptibility should stress maximum reflection. If the enclosure contains the RF source, the reflected RF energy inside the enclosure increases the internal circuit capacitive crosstalk, establishes standing waves in the enclosure accompanied with increased resonant amplification, and does not add fully to the overall shielding effectiveness.
An effective shielding design for an enclosure containing an emitter is very simple since the absorption loss (A) provides most of the shield attenuation. To enhance the attenuation, just add absorber materials. This approach works quite well at the higher RF and microwave frequencies because the shielding effectiveness is dominated by absorption loss.
Absorption loss can be calculated by:
where: AdB = absorption loss
Ka = 3.338 (t in mils) or 131.4 (t in mm)
t = thickness (mils or mm)
� = relative permeability
? = relative conductivity
F = frequency in MHz
Absorption is significant and continues to increase with frequency. The attenuation becomes so large that the shielding material does not normally limit high-frequency shielding effectiveness. A few examples will make this much clearer.
Typical absorption loss provided by a copper foil (� = 1, ? = 1) PCB enclosure would be 134 dB per mil of thickness at a frequency of 1,600 MHz. The foil thickness alone for a PCB shield would likely run 5 to 7 mils and could provide more than 670-dB attenuation.
But when the PCB enclosure is assembled, the attenuation typically is minimal. One of the primary reasons for the poor performance is the 0.2- to 0.5-mil thickness of the PCB ground plane. The PCB material, which makes up the bottom of the box, may only provide 33-dB attenuation.
In addition, this layer has multiple traces and holes. This may require a separate PCB enclosure located below the top box to augment the PCB ground-plane attenuation.
Another problem is that the shielding box on top also typically has holes. Unfortunately, holes are created by seams or needed by design elements that cannot be eliminated such as LCD displays, switches, keyboards, and controls.
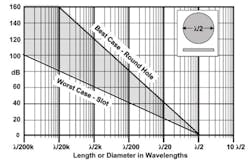
As a result, the calculated value for shielding effectiveness of the material represents a best-case value because it does not take into consideration the effects of holes and other discontinuities. The worst-case attenuation of a single hole or slot aperture that is not penetrated by a conductor in a thin conducting sheet is given by:
This equation can be solved in terms of L to determine the aperture size that results in a given attenuation. Figure 1 compares the shielding effectiveness of thin narrow slots vs. round holes. In general, apertures should be smaller than ?/50 and never bigger than ?/20.
To achieve acceptable attenuation values at 1,600 MHz, for example, apertures should be smaller than 4 mm. Although the smaller enclosures have potentially better shielding, their small size precludes the use of most standard RF gaskets so they must be soldered in place.
Nevertheless, size does matter, and the smaller the enclosure, the better it is. It is much easier to control the mechanical tolerances on a small mechanical device than on a larger one.
Ideally, there should only be one circuit per enclosure. This last criterion provides the greatest isolation between circuits and allows both the physical layout of the circuit and the shielded enclosure to be made as small as possible.
A circuit�s natural resonant frequency increases as its physical and electrical size decreases. Being small means that the frequencies have to be high before cavity resonance occurs.
At the enclosure�s resonant frequencies, the signals are passively amplified through the mechanism of cavity resonance. At a cavity resonance, the enclosure dimensions allow the reflected RF energy to add constructively or destructively to the incident energy.
The RF energy is reflected/re-reflected from the conducting surfaces of the enclosure, and the stored energy increases in magnitude until equilibrium is reached. At this point, the energy inside the enclosure dielectric volume has increased until the energy supplied by the source is equal to the energy absorbed by the interior surface area of the enclosure plus any power that exits the enclosure. This is a simplified restatement of Poynting�s Theorem.
Materials with higher conductivity have greater RF reflection and lower resistivity. Consequently, the better the RF shielding�right down to the RF gasket material�the worse the cavity resonance problem. For this reason, large shielded enclosures and cabinets for RADAR and microwave equipment have been using baffles and RF absorber materials to reduce reflections and enhance the absorption losses since the late 1940s.
A dielectric volume of any shape will exhibit resonance and represents the most general form of resonant cavity. The resonant frequencies are given by the following equation:
where: w, h, and l = the dimensions of the width, height, and length of the box
m, n, and p = the number of half-cycles occurring along a given
dimension
The cavity resonant frequency is inversely related to the enclosure size. The lowest resonant frequency will occur when the longest dimension is equal to ?/2. This is obtained when m = p = 1 and n = 0 and represents the Transverse Electric (TE) mode with one half wavelength across the width, none across the height, and one across the length, such as the TE101 mode.
Based on studies done on resonant cavities for reverberation chamber tests for MIL-STD-461 testing by USN Dahlgren, VA, the average RF field strength inside an unloaded reflecting cavity can be calculated by:
where: Q = the quality factor of the resonant circuit
Pin = power input in watts
?ant = antenna efficiency (0.9 for a horn)
ZO = characteristic impedance of the transmission
media = 120? for free space
CO = speed of light
Vvol = volume of the cavity (enclosure)
F = frequency in MHz
At resonance, the maximum increase in RF field strength inside the enclosure typically is 30 to 35 dB but can be as much as 60 dB. The peak field strength is 6 to 8 dB greater than the mean. Field levels are not uniform. At any given frequency, as the dimensions of the enclosure increase, more resonant modes are possible. Although the field levels increase, the variation from one point to another within the cavity is reduced for non-point-sized components.
Q values are proportional to the ratio of energy stored in the volume of the cavity to the energy dissipated in the impedance of the cavity�s internal surface area (Vol/As). For the same cavity configuration, using materials with the same magnetic permeability, such as 1, the Q values would be proportional to the ratios of the surface conductivity of the cavity.
At 2,000 MHz, an unloaded copper enclosure would have an unloaded Q of about 26,000 and a loaded Q of about 2,600. Loaded Q values typically are one-tenth (-20 dB) of the unloaded Q value. The extremely high Q values mean that the RF energy at the resonant frequencies exists in very narrow bandwidths.
As an example, for a resonant frequency of 3 GHz, the RF energy in the unloaded cavity would fall in a band that is only 0.115 MHz wide. Adding absorber material to the inside of the enclosure will reduce the Q and may solve the cavity problem. This is illustrated in Figure 3.
It is far better to make the enclosures so small that cavity resonance does not exist. If that is not possible, then add absorber materials. Don�t rely on the microwave absorber alone because the resonant frequency remains the same. However, the energy is spread over a wider bandwidth and the amplitude greatly reduced. The RF field amplitude and its Q value also decrease for any given enclosure as the frequency increases.
Shields can be made very small. Consequently, shielding is a very popular suppression technique for small, hand-held devices, especially those with RF oscillators.
The primary reason for shielding�s popularity is the belief that since shielding is not inserted into the circuit, it does not affect circuit operation and can be used at any time to solve emission and susceptibility problems without impacting signal integrity. That is true at the lower frequencies where the wavelengths are long enough that the shielded enclosure behaves only as a shield.
When the dimensions of the shield areUsed properly, shielding works well. However, it should not be used indiscriminately. Remember, shielding is not a mechanical solution to an electrical problem. It is an electrical solution.
About the Author
Ron Brewer currently is a senior EMC/RF engineering analyst with Analex at the NASA Kennedy Space Center. The NARTE-certified EMC/ESD engineer has worked full-time in the EMC field for more than 30 years. Mr. Brewer was named Distinguished Lecturer by the IEEE EMC Society and has taught more than 385 EMC technical short-courses in 29 countries and published numerous papers on EMC/ESD/PCB and shielding design. He completed undergraduate and graduate work in engineering science and physics at the University of Michigan. e-mail: [email protected]
January 2007