Behind the ADC Veil: Demystifying Common DC Specifications
Download this article in PDF format.
As its name implies, the function of an analog-to-digital converter (ADC) is to convert analog signals to digital representations for processing by a microcontroller (MCU), field-programmable gate array (FPGA), digital signal processor (DSP), or similar device.
In this article, we’ll review one of the most popular ADC architectures and how the dc specifications of a practical device differ from the ideal ADC model.
Sponsored Resources:
- TI Precision Labs - ADCs: DC Specifications: Input Capacitance, Leakage Current, Input Impedance, Reference Voltage Range, INL, and DNL
- TI Precision Labs - ADCs: SAR ADC Input Types
- TI Precision Labs- ADCs: Statistics Behind Error Analysis
What Does an Ideal ADC Look Like?
Regardless of how it accomplishes the task, an ADC produces a digital output from an analog input signal, a process known as quantization. Quantization error results from this process since a digital signal can only have discrete values, whereas an analog signal may have any value within the dynamic range of the signal.
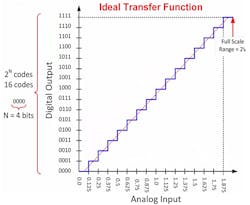
The quantization process leads to stair-step transfer function: Figure 1 shows this characteristic appearance in the transfer function of an ideal 4-bit ADC. This ADC divides the input voltage into 24, or 16, possible output codes, from 0000 to 1111.
1. The transfer function of an ideal ADC. (Source: TI Precision Labs—ADCs: DC Specifications video)
In general, an n-bit ADC has 2n output codes. For a full-scale output of 2 V, each increase or decrease of 0.125 V (= 2/24) at the input (VIN) causes an increase or decrease of 1 count at the output. VIN = 0 gives an output of 0000; VIN = 0.125 V gives 0001, and so on.
Each change from one code to the next takes place precisely at 0.125-V increments, so all of the steps are identical. Plotting the center points of each step yields a straight line.
The SAR ADC: A Data-Conversion Workhorse
Of course, although the performance of a real ADC comes very close to perfection (especially one of ours, LOL), several sources of error show up as deviations from Fig. 1’s ideal transfer curve.
There are many ways to convert an analog signal into its digital counterpart. All of them have different characteristics, but we’ll use the successive approximation register (SAR) as an example in this article because it’s suitable for a wide range of applications and is the default choice for general-purpose use.
SAR sampling rates typically range between 1 ksamples/s to 5 Msamples/s; resolutions can range up to 20 bits. SAR ADCs have very low power consumption, so they’re suitable for use in battery-powered applications. In addition, the power consumption scales with the sampling rate, so the SAR can achieve ultra-low power consumption at slow sampling rates.
A basic SAR topology (Fig. 2) consists of a sample-and-hold structure, an analog comparator, a SAR, and an n-bit digital-to-analog converter (DAC), where n is the resolution of the ADC.
2. The SAR is a widely-used general-purpose ADC architecture. (Source: TI Training: TI Precision Labs—ADCs: DC Specifications video)
The SAR conversion cycle has two stages—the sample phase and the conversion (or hold) phase:
1. During the sample phase, the ADC captures the input voltage to be converters. S1 is closed and S2 is open. An internal sample-and-hold capacitor (CSH) charges to AIN_P through RSH.
2. S1 opens; CSH stores the input voltage sample; and the conversion phase can begin. This has several steps:
- a. A comparator compares the sampled AIN_P to the output of the internal DAC; the DAC takes its input from the SAR. The most significant bit (MSB) of the SAR is initialized to 1 and all other bits are 0, so the DAC output voltage VCDAC = VREF/2.
- The output of the comparator feeds the SAR: if AIN_P > VCDAC, the bit remains at 1, otherwise it’s set to 0.
- The next most significant bit is then set to 1 and AIN_P is compared to the new VCDAC. This bit is set to the comparator output.
- Step c repeats until every bit in the SAR has been tested; the SAR then contains a digital representation of AIN_P.
The result is now available for use and a new sample phase can begin.
The n-bit DAC forms the heart of the SAR ADC. The standard architecture uses an array of capacitors with binary-weighted values to form a capacitive DAC (CDAC). Figure 3 shows a typical CDAC; a 5-bit converter is shown. Note that there are six capacitors: the MSB capacitor is on the left and there are two LSB capacitors so that the total capacitance is 2C.
3. A 5-bit CDAC architecture. (Source: TI Precision Labs—ADCs: SAR Reference Input—The CDAC video)
The operation of the CDAC is based on the principle of charge redistribution. A detailed description of its operation in the SAR can be found in this TI training video.
Real-World ADC Circuit Characteristics Affect DC Performance
Nonlinearities in any block directly affect the ADC’s performance. Let’s look at some circuit characteristics of a real device.
Input Capacitance
The value of the input capacitance (CIN), which is typically specified in the datasheet, depends on the mode of operation. For example, the ADS9110, an 18-bit SAR, has CIN = 60 pF when in sample mode, and CIN = 4 pF when in hold mode.
Why is this? Figure 4 shows a more detailed model of the ADS9110 sample-and-hold (S&H) circuit. The part has a differential input: it samples both AIN_P and AIN_N, so there’s an S&H circuit for each one with RSH = 30 Ω and CSH= 60 pF.
4. The model of the ADS9110 sample-and-hold circuit includes ESD structures and protection diodes. (Source: TI Precision Labs – ADCs: DC Specifications – Input Capacitance, Leakage Current, Input Impedance, Reference Voltage Range, INL, and DNL video)
In sample mode, S1P and S1N are both closed; therefore, CIN ≈ CSH: 60 pF typical. In hold mode, CSH is disconnected from the input pins. CIN then equals the parasitic capacitance of the input ESD diode structure, a typical value of 4 pF.
In a real-world device, the ESD structures and input parasitics also give rise to an input leakage current (IIL): a dc current that flows into or out of the ADC input pins. As shown in Figure 5, IIL can be modeled as a dc current source on AIN_P and AIN_N. The typical magnitude can range from nanoamps to microamps, and the current flow can be positive or negative; both magnitude and polarity can vary between devices.
5. The ADS9110 input model for leakage current.
As shown in Fig. 5, the leakage current can generate an offset error when it flows through any source impedance. For the 18-bit ADS9110 with a 5-V reference, a 1-µA leakage flowing through 10 Ω equates to an offset of 10 µV. That’s only 0.5 LSB for the ADS9110 but remember that ±1 µA given in the datasheet is only a typical value (see below for a discussion), so it could be considerably higher and still meet the specification.
Input Impedance
An unbuffered ADC has a switched-capacitor input stage, so its input impedance varies with frequency. The dynamic impedance depends on input leakage currents as well as the switching and charging of the input capacitance. The capacitive element doesn’t affect a dc input voltage, but it does affect the settling time when the input changes.
Some data converters include a front-end amplifier input that has a fixed input impedance set by the resistance of the gain-setting resistors. The ADS8681 in Figure 6 is one example: It’s a SAR ADC with an integrated programmable gain amplifier (PGA) and has a 1-MΩ input impedance.
6. The ADS8681 has a 1-MΩ resistive input impedance courtesy of its PGA buffer.
Adding an external resistance will change the gain of the amplifier. If this resistance is unknown or a dynamic impedance, it will introduce a system gain error, as discussed below.
Real-World Transfer Curves
The differences discussed above, and others, give the real SAR ADC a transfer curve that’s different from the ideal in Fig. 1. For example, mismatches in the CDAC—mismatches in the weighted capacitors, for example—are one of the leading contributors to nonlinearities in the transfer curve.
Since the ADC transfer function isn’t perfectly linear, one common means of evaluating it is to apply a linear fit curve to the specification being considered. The most common technique is an end point linear fit, in which the first and last points on the ADC transfer function define the straight line.
Figure 7 illustrates this approach applied to two common dc errors: offset error and gain error.
7. The linear fit method applied to the offset and gain errors. (Source: TI Precision Labs—ADCs: AC & DC Specifications video)
A straight line has the equation y = mx + b, where m is the slope of the line and b is the intercept on the Y-axis. The constant b is the value of the transfer function when x equals 0. In this case, it’s the offset error.
The offset error limits the available range for the ADC. A large positive offset error causes the ADC to output the maximum output code before the input voltage reaches the maximum limit. Conversely, a large negative offset error will cause the ADC to output all zeros before the input has reached the minimum limit.
The gain error is the difference between the ideal slope and the measured slope, expressed as a percentage. In many cases, this error can be eliminated with a simple two-point calibration. If an external resistance is added (Fig. 6, again), its value can be taken into account. You can find out more about this topic in the application note "Reducing Effects of External RC Filter on Gain Error and Drift in SAR ADC with Integrated AFE." Or consult TI’s Analog Engineer’s Circuit Cookbook, free to download.
Differential Nonlinearity
Differential nonlinearity (DNL) is defined as the maximum and minimum difference in the step width between the actual transfer function and the ideal transfer function.
As shown in Figure 8, DNL produces quantization steps with varying widths, some wider than the ideal value (positive DNL) and some narrower (negative DNL). An ideal device, of course, has a DNL of zero: All of the steps are the same size.
8. An ADC can exhibit both positive and negative DNL at different locations on the transfer curve.
In severe cases, the DNL can be large enough to cause a missing code. A code transition is completely skipped and that particular bit combination never appears on the output. Most modern ADCs are designed and tested to ensure that they will not have this problem. Datasheets often provide a no-missing-code (NMC) specification to highlight that the converter will not have missing codes.
Integral Nonlinearity
Integral nonlinearity (INL) is a measurement of how close the real-world ADC transfer function compares to a straight line. To eliminate the effects of gain and offset error, the measured transfer function is compared to an ideal straight line that’s fit to the endpoints of the ADC transfer function. The deviation between the ideal line and the measured function is the INL error. Again, the performance of the CDAC has a direct effect on the ADC’s overall INL performance.
In the 4-bit example shown in Figure 9, the green dashed line is the end-point fit of the transfer function. The green line starts at the first code, 0000, and ends on the last code, 1111. For a perfectly linear ADC, the straight-line fit would be directly down the middle of the ADC transfer function. The measured function, in blue, deviates away from the linear fit, so the ADC has a positive INL error.
9. These two methods are used to specify INL.
As with DNL error, the INL can be displayed versus the ADC output code in terms of LSBs (see Fig. 10 below for an example) or stated as a percentage of the full-scale range.
Decoding the Datasheet: The Statistics Behind the Numbers
The dc specifications we’ve discussed above are summarized in a table in the datasheet, plus several graphs that show their variation with temperature, reference voltage, and other parameters. Figure 10 illustrates the summary table for the ADS7043, a 12-bit SAR ADC.
10. A summary of the DC performance specifications for the ADS7043 12-bit SAR ADC. (Source: TI: “ADS7043 SAR ADC” PDF)
The semiconductor manufacturing process is tightly controlled, but there’s still a slight part-to-part variation. How do manufacturers ensure that the values given in the datasheet remain valid?
The minimum and maximum values are tested during production. To calculate a typical value, we turn to statistics. The Gaussian (or normal) distribution describes the distribution of physical quantities (e.g., datasheet parameters) that result from the combination of many independent processes, such as the steps in a semiconductor manufacturing process.
Figure 11 shows the Gaussian distribution applied to the offset error of an ADC. For a zero-centered specification, the typical value is the absolute value of one standard deviation plus the mean of the distribution. In this example, the mean is zero and the typical offset is ±1 mV; this corresponds to ±1 standard deviation. Since parts with values outside the minimum and maximum are discarded, the distribution is actually a truncated Gaussian distribution.
11. The statistical variation of many datasheet parameters shows a Gaussian distribution. (Source: TI Precision Labs—ADCs: Statistics Behind Error Analysis video)
It’s shown that 68.27% of the population falls within one standard deviation of the mean, but the other parts do not, so it’s wise to treat typical values with caution when performing design calculations. The maximum and minimum limits are set to minimize yield loss during manufacturing. Typically, the maximum is set above three standard deviations; 99.7% of the population is within this limit. In this example, the maximum was set to four standard deviations.
Conclusion
The SAR architecture is widely used for analog-to-digital conversion, but the performance of a real-world device deviates in several ways from that of an ideal model. This article has provided insight into some of the common dc specifications in the SAR datasheet.
In addition, even though many datasheet specifications are guaranteed, certain parameters are listed as typical values without minimum and maximum values. This article has also reviewed the statistics behind these parameters.
Sponsored Resources: