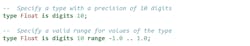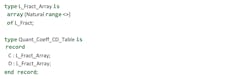Assessing the Ada Language for Audio Applications

GNAT compiles Ada sources directly into machine code. The performance of compiled code is generally comparable to that of C, as shown in (Gouy, 2016).

For this report, we mostly used the GNAT Pro version of the compiler.

Porting of Layer-2 Decoder Implementation

To evaluate the various features of the Ada language for audio applications, we decided to use an existing implementation as the starting point instead of writing small prototypes. Our expectation was that this would provide a better understanding of the issues that developers might encounter and an illustration of how the Ada language can be used in these situations.

We decided to use an existing implementation of an MPEG-2 Layer-2 decoder (International Organization for Standardization, 1993) (Brandenburg & Stoll, 1994). This reference implementation was written in the C language and ported to the Ada language.

That C implementation is based on a separate framework that models mathematical operations. This framework is called Intrinsics. It allows for using either fixed- or floating-point operations.

Due to the native support in the Ada language for fixed-point data types and arithmetic, an additional goal of the evaluation was using those native data types and comparing them to the Intrinsics used in the C implementation.

Porting work

Many approaches can be used when porting an implementation. For this work, we created a new, ported implementation from scratch by using the original code as a reference and for regression tests. Source-code examples taken from the Ada implementation of the Layer-2 decoder are presented in various sections of this report.

For the regression tests, both reference and ported implementations were run and the input and output data of selected parts of the implementation were compared.

In general, the porting of the Layer-2 decoder implementation from C to Ada was straightforward. The Ada compiler and the Ada language itself made the job easier, because many errors could be detected at compilation time and by automatic run-time checks. Details about the Ada language will be discussed later.

Some optimizations of the underlying mathematical operations of the Ada implementation were performed. But they were limited to function inlining. Other kinds of optimizations, e.g. using inline Assembly, were skipped. The performance of both reference and ported implementations was measured on a PC. In this case, the performance of the Ada implementation was comparable to the C implementation.

Testing against reference implementation

Testing of the Ada port against the reference implementation was made with 365 bitstreams in Layer-2 format. This set contained bitstreams in mono and stereo channel modes. Also, it contained bitstreams with 24- and 48-kHz sampling rates.

We have compared the implementation in two cases. The first one was when the reference and ported implementations used fixed-point arithmetic for the DSP algorithms. The second one was when both implementations used floating-point arithmetic for the DSP algorithms.

Differences between implementations were measured in least-significant bits (LSB) based on decoded wavefiles containing 16-bit pulse-code-modulation (PCM) data. The table below presents the root-mean-square (RMS) differences:

Typically, RMS differences up to 1 LSB are considered acceptable. Therefore, the Ada port has successfully passed this test.

Stability testing

Stability tests were performed using erroneous bitstreams, which simulate transmission errors that can occur, for example, in noisy communication channels. Due to the complexity of the bitstream syntax, it may be particularly hard to fully identify potential error cases in unit tests. Thus, erroneous bitstreams may uncover bugs that cannot be detected otherwise.

These erroneous bitstreams were created by using a tool called erand, which randomly flips bits based on an input “bit error rate.” Two rates were used: 1⁻³ (corresponding to higher error level) and 1⁻⁴ (corresponding to lower error level). In this case, erand was applied on the bitstream set mentioned above, thereby creating two sets of erroneous bitstreams.

The same sets of erroneous bitstreams were used to test both the reference and ported implementation. In all cases, no issues were found.

Numeric Types of the Ada Language

In this section, we present the numeric types of the Ada language, focusing on their application for digital signal processing algorithms.

Expressions and arithmetic

Ada is both a statically typed (like C and C++) and strongly typed language (unlike C and C++). The consequence of that is implicit-type conversions are almost completely absent in the language and completely absent as far as arithmetic is concerned. Every conversion must be performed explicitly.

This is more restrictive than C and C++, where implicit numeric coercions are allowed in a number of places. Still, it’s a good way to make sure that everything about the program’s computations is explicitly specified.

Implicit conversions and conversions rules are a common source of errors in C and C++. Ada was designed to make sure that the meaning of every potentially ambiguous operation was explicitly specified by the developers.

Ada has all the operators expected by C developers: Addition, subtraction, multiplication, division. It also has an exponentiation operator, **, a true mathematical modulo operator mod, and a C-style modulo rem.

Numeric types

One of the distinctive features of Ada with regard to arithmetic is the extensive possibilities of defining numeric types.

Where in C and C++, int, long, and other types are built-in opaque types, Ada allows developers to define their own numeric types. Also, the standard types are defined in a straightforward manner using the language’s syntax.

Ada provides custom accessors, called attributes, to access specific properties of the type:

Overflow

One of the most dangerous pitfalls in digital signal processing is the behavior of numeric types when they overflow. The C language standard defines overflow as being undefined behavior on signed types.

In Ada, the behavior is specified in the language definition and depends on the type:

• With signed discrete integer types, if an operation overflows, an error is raised.
• With unsigned modular types, if an operation overflows, the result will wrap. This result isn’t limited to built-in types and also works for types with arbitrary bounds.

Floating-point types

To define a floating-point type, the required information is the relative precision or, in other words, the number of digits that will be stored:

This facility is a major benefit of Ada over the C and C++ languages. In C/C++, developers have the choice between float and double. The usual reasoning is that float is chosen if accuracy isn’t important and double is chosen if it’s important. In either case, developers can’t be certain of the accuracy they will get because it’s platform-dependent.

In Ada, developers specify the accuracy needed for the specific algorithm being written. The compiler will choose an appropriate floating-point type with at least the accuracy required. This way, the requirement is guaranteed. Moreover, if the computer has more than two floating-point types available, the compiler can make use of all of them.

Fixed-point data types

Ada also has the ability to declare and work with fixed point types:

Here, we’re defining an Angle type whose values can range from -Pi to Pi. The delta indicates the minimum accuracy, so that the compiler can safely use 32 bits for variables of this type.

The use of fixed-point data types for DSP algorithms will be discussed in Fixed-point data types for DSP.

Operating overloading

Ada also allows developers to define custom behavior for common operators. In this way, they can define custom numeric types that behave in a specific way, e.g., saturating arithmetic floating-point types.

Unlike C++, Ada is pretty restrictive in the set of operators it allows developers to overload. Only a subset of operators can be overloaded.

The aim is to draw a line: Allow developers to overload the most useful operators and be able to define new abstract data types with expressive APIs, but forbid use cases where the built-in language semantics would be altered in a way that’s confusing for the developers.

Unlike in C++, it’s impossible, for example, to overload the assignment operator or the function call operator. This is consistent with one of the tenets of Ada, which is to produce readable source code. One of the elements of readability is predictability. The code should not have a hidden meaning that’s not apparent to the developers. Overloading semantics such as those of assignment, short-circuit Boolean logic, or function calls violate this principle. Hence, they’re not allowed.

Data types for DSP

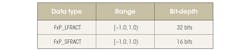
Algorithms for digital signal processing typically make use of data types normalized to the range [−1.0, 1.0), especially when targeting fixed-point implementations. The original implementation of the Layer-2 decoder is based on this numerical range. More specifically, it makes use of the data types presented in the table below:

As becomes clear from the table, the only difference between the data types is the bit-depth. The range is the same in both cases.

Fixed-point data types for DSP

As in most programming languages, C doesn’t provide support for fixed-point data types. Therefore, the data types above need to be represented by using integer data types.

As we have previously seen, unlike most languages, Ada provides support for fixed-point data types in the language specification since its first version. Also, it allows for specifying the accuracy using the attributes Small and Size (Barnes, 2014, p. 430, Location 11199).

For the data types used in the Layer-2 decoder, we used the following specification:

Ada also provides operators for fixed-point data types. For example, the following code makes use of a fixed-point multiplication using the data types specified above:

We can also use mixed-precision operations:

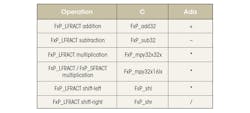
In the original reference implementation of the Layer-2 decoder in C language, operators had to be manually defined. For example, a fixed-point multiplication is defined in the function FxP_mpy32x32x(). In the ported implementation, these operators were replaced by the corresponding mathematical operators natively supported by the Ada language. A side effect was that the readability of DSP algorithms in the ported implementation was much better than in the original implementation in C. The table below presents the conversion of typical fixed-point operations from C to Ada: 

Saturation

Unfortunately, the Ada language doesn’t directly support saturating operations typically used in algorithms for digital signal processing. Therefore, these operations have to be modeled, as is the case in the C language. However, in the case of the Ada language, readability needn’t suffer—it’s possible to overload operations so that the mathematical operators can still be used. In summary, mapping saturating operations in Ada involves one of two basic approaches:

1. Use existing data types and define saturating functions for them. For example, this is the declaration of the saturating addition for the L_Fract type:

2. Use derived data types for saturating operations and overload the operators. For example, this is the declaration of the saturating addition for the new L_Sat_Fract type:

Since readability is an obvious advantage here, we selected the second approach for our porting work. In this case, we introduced two new data types for saturating operations: L_Sat_Fract and S_Sat_Fract. When saturating operations are needed in the implementation, variables can be easily converted to the corresponding saturating data type. This will not affect performance, since no code needs to be generated for this conversion. For example:

Extending with floating-point operations

In the previous examples, the data types were targeting implementations that make use of fixed-point operations. However, when writing algorithms for DSP, it might be advantageous if the same source-code can be compiled to use either fixed- or floating-point operations. In other words, to reduce future maintenance, it might make sense to avoid having two separate implementations: one for fixed-point operations and one for floating-point operations. Instead, the same source-code could cover both cases. As long as the numeric range mentioned above is respected, this type of universal implementation can usually be achieved.

There are two options when it comes to abstracting the algorithm from the numeric data type:

1. Use Ada’s generics to make the entire decoder generic on the numeric type. The decoder will then work on a generic type with a set of abstract operations. The type and the operations will be replaced by a specific, instantiated type with a set of specific operations when developers instantiate the decoder.

2. Use compile-time constants grouped in separate Ada packages. One of the packages is used at compilation time depending on which kind of numeric operation is selected.

For the port of the decoder, we used the second approach. Details about these approaches are discussed in Numeric abstraction using Ada packages.

Control Structures and Subprograms

Control structures

Ada replaces the C for loop with more structured iteration styles:

This style suppresses whole classes of bugs. For example:

• For loops not terminating because the wrong variable is being incremented
• Uninitialized iteration loops
• Assignment instead of equality in the loop condition

Subprograms

Ada has two kinds of subprograms: functions and procedures. Functions are subprograms that return a value, and procedures are subprograms that don’t have any return value. It’s impossible to ignore the result of a function in Ada:

Procedures are equivalent to functions returning the special void type in C. In Ada, unlike in C, if a subprogram is calling a function, it has to explicitly process its result. This encourages:

• Safety: The return value of a function has a meaning. If the subprogram decides to ignore a result, then this needs to be explicitly indicated—it’s not possible to do so unintentionally.
• Readability: If developers decided to ignore a result, a subsequent reader of the code will immediately be aware of that.

Parameter modes

Another feature that distinguishes Ada from the C and C++ languages is parameter modes. In Ada, subprogram parameters are either passed as in, in-out, or out parameters. The in parameters are only meant to be read, in-out parameters are meant to be read and written, and out parameters are only meant to be written.

This means that, where C developers would have used pointers to emulate an out parameter, Ada developers can use an out, or an in-out parameter. Thus, they can specify to a higher level the way their API is intended to be used.

Reducing the use of pointers and dynamic memory allocation as much as possible is an important design goal in Ada. Parameter modes help achieve this goal. Here’s an example extracted from the decoder implementation:

By specifying the mode of each parameter, we structurally eliminate whole classes of bugs:

• If developers try to read from AD within the procedure Get_Audio_Data instead of writing, the compiler will produce a warning.
• If developers try to write into Info within the procedure Get_Audio_Data, the compiler will produce an error message.

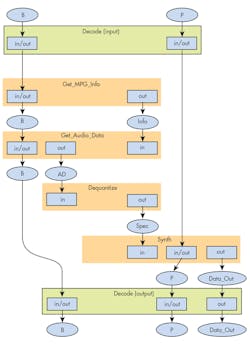
Also, the Ada language allows developers to clearly specify the data flow of the implementation. In the example above, AD (of Audio_Data type) is an output parameter of the procedure Get_Audio_Data and an input parameter of the procedure Dequantize. Likewise, S (of Spectrum type) is an output parameter of the procedure Dequantize and an input parameter of the procedure Synth. The implementation can then be analyzed to derive the complete data flow:

Information based on the implementation of Decode and the specification of the subprograms called by it derives the data flow in the figure.

Data flow of decode.

Parameter modes aren’t supposed to specify anything about whether the parameters are passed by copy or by reference. This is left to the Ada specification and compiler, which makes the most efficient choice depending on the platform and the data type. The Ada Reference Manual specifies that elementary types are always passed by values, and leaves the choice to the compiler for composite types. This removes yet another source of potential ambiguity in the use of pointers in C:

In the example above, spec might be passed via a pointer, because:

1. It’s an array.

2. It’s mutated in the function synth.

3. It’s a big struct. Therefore, it’s passed by reference to improve performance.

The actual reason for the use of pointers in the previous example in C might be a combination of the above. Also, in the previous example in Ada, it was shown that spec is actually a read-only parameter. In contrast, this important information is lost when using the C language. Developers might indicate this in comments, but, if so, a static-analysis tool can’t use this information to detect bugs, and comments aren’t checked by any automated tool, so they can become desynchronized with the code.

Ada and static analysis

As we’ve demonstrated with parameter modes, and as we will demonstrate in the remaining part of this report, Ada encourages developers to specify as much as possible about the behavior of their code. The philosophy is to attach as many specifications as possible to the code. This information can be used in the following manner:

• The compiler can use this information to give exhaustive and precise error messages.
• The compiler can use this information to give even more exhaustive warnings about possibly erroneous code.

As an instance of this, the GNAT compiler is able to detect a very large category of erroneous code patterns. When warning checks are activated, the GNAT compiler can be considered a lightweight static analyzer on its own, as evidenced by the complete list of warnings (Free Software Foundation, 2017).

• Custom static-analysis tools can use this information to provide more detailed diagnostics. The fact that developers can provide custom ranges for numeric types, for example, allows static analyzers to detect out-of-range errors that would be impossible to detect in C/C++, simply because the allowed ranges aren’t known by the tool.

Likewise, in the code example presented in Parameter modes, we outlined an area where the compiler would be able to issue a warning for writing into an array parameter that was specified as an input parameter. The compiler will not be able to emit a warning on complex cases, for example, as soon as developers write to the array. However, a more sophisticated static analyzer will be able to tag all values contained by the array as uninitialized, and track their use via control-flow analysis/value tracking.

Arrays and Records

Arrays

The use of arrays in Ada is safer and more flexible than in C and C++ languages. In Ada, arrays are first-class data types. In contrast, arrays in C/C++ have several limitations:

• Their size must be fixed at compile time. The C99 standard added variable length arrays, but they can’t be passed as parameters or returned from functions.
• In most contexts, arrays in C and C++ are converted to pointers, so developers lose information and safety when using them. For example, bounds aren’t part of the type or instance. Also, the very information that the instance is an array is lost.
• As a consequence, the essential information of the bounds of the array must be passed by developers or the length recalculated every time, as is done for strings in C.
• There’s no option to bound check arrays in C, so an out-of-bound access will result in undefined behavior.

Ada solves these limitations by making arrays a first-class construct:

• Ada arrays always include their bounds. Out-of-bounds accesses result in an error.
• Array length can be determined at runtime, depending on runtime variables.
• Subprograms can return arrays and take arrays as parameters.
• Unlike in C, where there’s no notion of an indexing type, developers can choose the type by which the array is indexed in Ada.

The following example presents a type definition for an array and its use as an output parameter:

In this example, the type PCM_Channel_Buffer defines an array of PCM values. In this case, PCM is a new type based on S_Fract. The type PCM_Channel_Buffer is indexed by the Natural type. This means that the minimum index of PCM_Channel_Buffer instances is 0, and the maximum index is 2³² − 1. Here, the <> symbol means that the range of instances isn’t known, but will be determined dynamically. Also, the function Synth_Channel will initialize every element of the PCM_Channel_Buffer.

If we contrast this example with the equivalent one in C language, it becomes clear that the specification in Ada is much more precise than the version in C:

By looking at this function declaration, it’s impossible to tell whether data_out is a pointer to a single element or an array, or if it can be set to NULL or not. Also, the length of the array needs to be passed explicitly. In the Ada version, the length information is implicit in the PCM_Channel_Buffer type.

C++ high-level containers, such as std::vector, offer the same expressive power as Ada arrays, but to the detriment of performance. The elements of std::vector are allocated on the heap, whereas Ada semantics allow all of the arrays to be allocated either on the stack or on stack-like memory areas, leading to very efficient memory management.

It’s possible to assign to array components and read their values through the same notation that’s used for subprogram calls:

Using Ada to write correct algorithms

The previous subsections presented Ada features that make it possible for developers to write safer applications. This subsection presents the interaction of these features when used together and how they allow developers to detect more errors during compile-time.

Consider the following example in C:

There are a number of errors or ambiguities in this example:

• The result is specified as float*. But it’s not possible to tell without reading the documentation if there’s any result, whether this is a statically allocated array, a dynamically allocated array, or a pointer. It might even be a null pointer.
• The array parameter suffers from the same ambiguity in the function specification. This means that, if developers don’t have access to the code and if the documentation isn’t up-to-date with the implementation, errors can be made because of specification problems, e.g., not handling null-pointer results.
• The size is supposedly the size of the array. Again, the documentation will be the guide to the developers. The size might be negative or zero and the developers have to interpret what that might mean.
• The for-loop specification is incorrect: It goes one element too far. Since no connection exists between the array parameter and the size parameter, there’s no way for the compiler to make the connection between the two and, hence, be able to emit an error.
• New values are being assigned to the tab̀ variable in the loop. This variable was supposedly only meant for input, but it’s impossible to verify because developers have no way to specify that fact.
• An integer value is being multiplied by a float value. The specifics of how and when which value is converted is hard to decipher by reading the algorithm.
• The function returns a pointer to an array allocated on the stack. In this case, however, it won’t be valid when the caller tries to use it.

The problem is such that, even when running a state-of-the-art C compiler on this code with all warnings activated, developers might not get a warning for every error. That’s because the compiler simply doesn’t have enough information to detect that the code isn’t correct.

This is the equivalent code in Ada:

• It’s clear that the return value is a newly allocated array of float elements. The size is included in the array. There’s no null value possible.
• The same applies to the Tab parameter.
• The bounds are part of the array, therefore it’s correct by construction.
• For the same reason, we can’t iterate one element too far in the loop.
• Since Tab is an input parameter, modifying its content in the for loop will trigger a compilation error. Similarly, since we’re using an uninitialized Tab2 array and reading its values, a warning will be emitted.
• The multiplication of an integer value by a float value will be detected and trigger an error.
• The return value is a first-class array value. It will still be valid in the caller.

Table of fixed-point data

This subsection presents an example of how Ada’s arrays and fixed-point data types can simplify the representation of tables. This was the original table from the C implementation:

In this example, a macro (FRACT) is used to convert the values from floating-point to the fixed-point representation. In the case of Ada, no macro is needed because of native support for fixed-point data types:

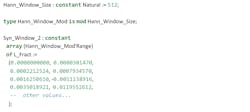
Also, in the case of the Ada language, we can define a data type for the range (Hann_Window_Mod). This allows for automatically verifying that all accesses to the Syn_Window_2 table are in the correct range, thereby eliminating invalid memory accesses in other parts of the application.

Automatic range checking

The working assumption when using the bitstream set mentioned in the previous section for testing was that all bitstreams were correct (i.e., conformant to the Layer-2 standard). However, surprisingly, there were actually some bitstreams in this test set that contained non-conformant information.

In fact, the Layer-2 standard defines a scalefactor index table ranging from 0 to 62. In the case of the non-conformant bitstreams, this index was set to 63. This issue went undetected by the C implementation, while the Ada implementation raised an exception for it. This check was possible because in the Ada implementation, the scalefactor index was defined as a range:

The corresponding check took place in the call to Get_Coefficient, where the function verified that the argument was in the range specified in the Scalefactor_Range subtype:

As a comparison, the reference C implementation looked like this:

In the case of the C implementation, a manual range check of the value from the bitstream was missing.

In general, the strategy of specifying ranges in the Ada code makes it possible to automatically check the values from the bitstream. Naturally, this requires extra effort, as discussed in (Ben-Ari, 2009, location 329):

Effective use of Ada’s type system requires an investment of effort on the developer’s part:

• During the design of the software system, the developer must select types that best model the data in the system and that are appropriate for the algorithms to be used. If a program is written with every variable declared as Integer, Float or Character, it will not be taking advantage of the capabilities of Ada.

Enumerated types

Like C, Ada allows the definition of enumerated types:

Unlike C, Ada’s enumeration types are strongly typed:

In the example above, A cannot be used to initialize B because their data types do not match.

Since enumerations are regular discrete types, enumeration types can be used to index arrays, which create some expressive options in the use of arrays:

This approach also ensures that all values in the Sampling_Rates_Mpeg range have a corresponding value. Naturally, this enumeration can be used to access the table.

Record types

Ada allows developers to define composite types, composed of distinct data fields:

This is the equivalent declaration in C:

Record types largely behave like structs in C. However, they have additional features, as will be demonstrated in the next subsection.

Discriminated records

It isn’t possible to put arrays of indefinite size in records in Ada, because the compiler needs to know the size of instances of the records. It can’t do so if there’s an unknown size array as a field:

Because the actual range of L_Fract_Array type isn’t set for elements C and D of the Quant_Coeff_CD_Table record, the compiler can’t know its actual size. This causes a compilation error.

In C and C++, developers would have one of several choices at this point:

• Use a fixed size for the L_Fract_Array type. This would work correctly. However, the approach hampers code reuse because if the developers needed a buffer of a different size, they would need to duplicate the definition and associated code.
• Use heap allocation, either by using malloc for the buffer, or by using a high-level container like std::vector.
• In C++, developers could use templates to parameterize a type depending on the size. This has its own set of drawbacks that will be discussed later. In this case, though, one of them is template propagation: Every algorithm that would need to work on a L_Fract_Array of any size would also need to be a template. The typical associated problems with this approach are compilation time and code complexity, for example.

In Ada, it’s possible to make the exact shape of a record depending on one or several special fields, which are called discriminants. Here’s how we may rewrite the previous example in correct Ada code:

In this example, the size of the contained array depends on the value of the Size discriminant. In this way, it’s possible to make a fully functioning composite type that will have following characteristics:

• This works without any heap-allocation: instances can live entirely on the stack, with associated performance and safety benefits.
• There’s no need to use generic programming in this case.

Avoiding heap allocation

As explained in the previous section, Ada allows developers to precisely model by-value types and pass them as parameters to subprograms and as return values. This, in turn, allows Ada developers to avoid heap allocation in many situations where it would have been necessary in C and C++. This subsection elaborates on the advantages of this approach.

Safety

The first and foremost reason is for safety. The lifetime of heap-allocated values is impossible to determine statically in the general case and it’s easy to make errors that create hard-to-find and hard-to-reproduce bugs. While there’s a lot of research on how to find a paradigm in which heap allocation is safe, it’s still a research topic with no clear answer (Hicks, Morrisett, Grossman, & Jim, 2004). In C++, some types encapsulate unsafe memory management in a mostly safe interface. However, it’s still relatively easy to have memory issues such as referencing an already deallocated value of the vector.

Performance

Heap allocation is generally very costly in terms of runtime performance when compared to stack allocation, and has complicated performance behavior depending on the whole application (Detlefs, Dosser, & Zorn, 1994). Also, on most operating systems, heap allocation involves a system call, which has its own overhead. Stack allocation, on the other hand, is both cheap and predictable in terms of performance.

Aggregate literals

Ada has a powerful notation for inline initialization of composite data structures such as arrays and records. Here is, for example, how it could be used to initialize an instance of the Meta_Info record defined previously:

This notation can also be used with arrays:

In this case, the Subband_Samples can be either initialized by using the others keyword or by using an explicit for loop.

This notation can be used as a very powerful data-declaration language. Here’s an example, extracted from the decoder, of how it can be used to fill a table of sampling-rate conversions:

One big advantage of this notation in terms of safety, similarly to case statements and expressions, is coverage checking. In the last example, when initializing Sampling_Rates_Mpeg, if the developers didn’t fill the information for Mpeg_2_5, the compiler would have issued an error.

Abstraction and Modularity of the Ada Language

Packages

Ada supports modular programming in the form of packages and subpackages. The closest C and C++ get to modular programming is an approach based on file inclusion via the preprocessor, which uses #include directives. In Ada, however, there’s no standard support for a preprocessor. Consequently, the mechanism to organize source code into different units isn’t a simple text inclusion system, but rather a real module system.

Below is an example of what a package looks in Ada:

As shown in this example, the basic mechanism for privacy and encapsulation isn’t at the type level, as is the case in C++ or Java, but at the package level. Everything that follows the private qualifier isn’t accessible to the user of the package. For the user, Polyphase is an opaque type, with operations on it exposed as subprograms.

Using a module system rather than an inclusion system has a number of positive consequences for the developers and the compiler:

• The application can be decoupled into separate namespaces, depending on the functionality or domain. In C, there’s only one global namespace and lots of possible name clashes. This effect needs to be taken into account by the developers. In C++, the namespace system is decoupled from the file inclusion system.
• It makes it possible to get rid of the common limitation of text inclusion mechanisms, such as include guards.
• It allows for much faster analysis by the compiler: Each time a file is included in C, the compiler has to reanalyze it entirely because its interpretation potentially depends on the surrounding context (such as definitions and macros). In Ada, a package need only be analyzed once. The compiler can cache the result of the analysis because it knows the correspondence between a package name and a file name, and between a package specification and a package body.
• The above allows many features to be made possible at the language level. Since the compiler has more precise information about the code of each function, it has better potential for optimization.

Generics

Ada has full support for generic programming. As a result, developers can make either a subprogram or a whole package become parameters of an abstract entity; for example, a type, an object, or a set of functions. This is very similar to the concept of templates in C++:

In the above example, we’re specifying a generic package. It’s generic on two types, which we define as being any signed integer type. The first type defines the range of the buffer and the second type defines the range of the buffer’s channels.

In Ada, it’s possible to declare generic packages and subprograms. The specification and the body both need to be declared in each case. The specification lists the generics arguments, which are omitted in the body.

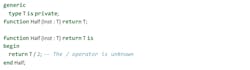
Unlike templates in C++, Ada generics are statically typed before they’re used, so that, for example, this is illegal:

In this example, the division operator can’t be used, because it’s not defined for the private type T. In order to use an operator or a function on a private type, developers have to include it in the specification of the generic:

This is consistent with the other design divergences between Ada and C++. Ada forces developers to specify their code more precisely, producing gains in diagnostic quality and usability. Since generics are checked immediately, before instantiation, nested generics cause fewer problems in terms of diagnostic quality.

A big difference between C++ templates and Ada generics lies in the instantiation—in Ada, it’s necessary to explicitly instantiate a generic before using it:

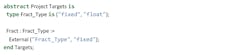
In the above example, L2_Audio_Data is a package instance based on the generic package Audio_Data. Although the use of generics might make the code more verbose, it gives developers more control over the generated code, which is important in safety-critical contexts.

Generic packages can also be reused as parameters of other generic packages. For example, the generic Audio_Data package specified above can be used as a formal package in another generic package:

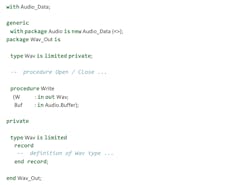
In the Layer-2 decoder implementation, Wav_Out can be instantiated with the L2_Audio_Data package, which was defined above as an instantiation of Audio_Data:

The way generics are architected in Ada makes it easy to conceive of whole units of code as being generics, because developers get semantic checks based on the contracts that they have specified in the generic section. The Ada compiler checks, for example, if the data types have the required operations and if the operators are being used for the correct types.

Numeric Abstraction with the Ada Language

As discussed in Extending with floating-point operations, algorithms for DSP can benefit from numeric abstraction. This section provides details on two approaches that can be used to achieve this abstraction.

Numeric abstraction using Ada packages

This subsection describes the use of Ada packages to abstract numeric operations. What follows is an example of the declaration of the data types for floating-point operations:

Note that the Is_Fixed_Point constant is needed in the few locations of the source code where the same implementation doesn’t work for fixed- and floating-point operations. Therefore, two distinct options are needed.

The selection of the underlying data type (floating- or fixed-point type) is made at build time. The build system has an option that allows developers to select the type. In the case of the Ada language, this can be implemented by using a GNAT project file built with the gprbuild system (AdaCore Inc., 2017). GPRbuild is essentially a GNAT tool for building Ada applications. It’s based on a project formalism (the GNAT Project File) that describes in a declarative form a list of sources and options to build executables and libraries. For example, the following project declares a configuration variable for the data type:

This variable will then be used to select files to link with at build time. One set of files for fixed point and one set for floating point:

The only difficulty that may show up when writing universal numeric code using Ada is that the multiplication and division operations have a special definition for fixed-point data types, as specified in Ada Conformity Assessment Authority (Ada Conformity Assessment Authority, 2012, p. 120, Chapter 4.5.5 (18-19)) and discussed in (Ben-Ari, 2009, Location 2518). This definition is different from the one that applies to floating-point data types. Consequently, it’s slightly more difficult to write universal source code when compared to targeting just fixed-point operations. In most cases, though, being careful about the data types is enough to get the implementation working for both fixed- and floating-point targets.

For the porting of the Layer-2 decoder, the Ada implementation was first completed using just fixed-point data types. The adaptations to make it work with floating point were performed at a later stage. They were restricted to just a few locations in the source code; most parts of the implementation didn’t require any change.

Below are a couple of examples of adaptations:

• In the wavefile writer, for the implementation based on floating-point arithmetic, the PCM data (in floating-point format) needs to be converted to an integer representation before writing the data into the output file. In the case of the fixed-point version, the PCM data can be directly written to the file.
• When parsing spectral data from the bitstream and storing into the buffer, the data needs to be converted using different methods. In the implementation using floating-point buffers, the spectral data from the bitstream must be converted from an integer format to a floating-point format. This step isn’t necessary in the version using fixed-point buffers.

Numeric abstraction using Ada generics

This subsection describes the use of Ada generics to abstract numeric operations. We first discuss the generalization of individual subprograms, and then get into the generalization of the whole decoder.

Selectability using Ada generics

An example of using Ada generics for numeric abstraction is when different implementations of an algorithm are combined into a single, generic version.

For example, two versions of the fast Fourier transform (FFT) are used in the Layer-2 decoder: one makes use of saturating operations; the other scales the input values down to avoid using saturating operations. In the original implementation in C, both versions are implemented in the same function. In this case, preprocessing flags are used to select one of these versions at build time.

Ada generics can be used to implement a more elegant solution. This is the corresponding specification of the FFT:

In this example, we declare new data types based on L_Fract and S_Fract. When later instantiating Fft_Main_Loop, these types can be initialized with the non-saturating version (L_Fract and S_Fract) or the saturating version (L_Sat_Fract and S_Sat_Fract) of the data types. The associated operators need to also be passed to the generic procedure.

The operators to be used in the instantiation may then be defined as follows:

The first two definitions (Mult_LL and Mult_LS) make use of the standard fixed-point operators. The remaining definitions (Mult_LL_Sat and Mult_LS_Sat) simply refer to the corresponding operators defined in the Fractional.Sat package. In this case, Ada subprogram renaming is employed using the keyword renames.

Two instances of the procedure can then be instantiated by associating them with the corresponding data types and operators:

The selection can later be made at build time by using a constant Boolean value:

Generalizing to the whole decoder

This subsection describes the use of Ada generics to abstract numeric operations. In Numeric abstraction using Ada packages, we have shown how the decoder’s implementation was made to work with both floating-point and fixed-point data types.

It would also have been possible to make the entire decoder code generic on the numeric type. The advantage of this approach would have been to be able to instantiate several decoders with different data types in the same code base. While this wasn’t necessarily useful for the case of the Layer-2 decoder, it could be useful for certain applications.

However, after experimenting with this approach, due to limitations in the Ada generic model, the code also gets somewhat more complex:

• While it’s possible to have a generic type that’s either a floating- or fixed-point type, doing so requires specifying it as a private generic type, which in Ada generics, can mean any type—numeric or not.
• This, in turn, forces developers to pass around operators for the private type, because the compiler has no knowledge of the built-in numeric operators of this type.
• Constructing values of the type would require the use of a special constructor, because the compiler doesn’t know that real literals are valid for this type.

An example for third bullet point above is:

For those reasons, while it’s possible to have an implementation of the decoder that’s completely generic, it has been deemed too complicated for the benefits to be in the scope of this work.

Multithreading and Parallel Programming

Tasking

Ada has built-in facilities for multithreading. In C, threads are added as libraries on top of the languages. In contrast, threads in Ada, which are called tasks, are a native concept. At the simplest level, Ada tasks follow the basic thread abstraction—tasks correspond to distinct threads containing code that runs concurrently.

In the example below, the procedure Synth calls a DCT-II for each spectral slot to be processed:

Since there’s no dependency between the individual slots, we can process the slots concurrently. To do that, we can wrap the call to the DCT in a task type:

In this example, we define the task type DCT_Task and an array of tasks Dct_II. Rendezvous points allow for interaction with these tasks and are indicated by the keywords entry in the task specification and accept in the task implementation.

In the example above, we have two rendezvous points: Start and Finish. As soon as all threads have been started after completing the first loop on Dct_II, they run concurrently. The second loop on Dct_II waits for all threads to finish so that the remaining process in Synth can be performed.

This demonstrates basic synchronized interaction with a task. The key point is that as long as the user interacts via task entries or via protected objects, the interactions are synchronized. There’s no need to use mutexes, semaphores, or other synchronization objects in the common case.

A full detailed description of the Ada tasking model is beyond the scope of this report. What’s interesting is that developers can design safe, concurrent programs without relying on third-party libraries. This will also make portability to embedded platforms easier, since concurrency has to be handled by the compiler, not by the developers.

Parallel programming

In the domain of DSP, parallel execution of algorithms is an important topic. The Ada Rapporteur Group, which is the group in charge of the standardization of the Ada language, is currently working on a set of features to make parallel programming in Ada easier (Ada Rapporteur Group, 2017),  (Taft, Moore, Pinho, & Michell, 2016).

This will allow developers to express parallel loops, for example, with a straightforward syntax. As of today, the syntax isn’t finalized, but the intent is to be able to write these in the following way:

In that example, the compiler takes care of parallelizing the calls to the DCT-II.

Looking ahead, once integrated in the language and implemented by tools, these capabilities will allow writing code that can selectively run on either a main process or co-processors. It would be similar to what’s done today with C extensions like CUDA, OpenMP, or OpenCL, but integrated directly into the definition of the language. This will allow Ada developers to easily take advantage of co-processors that specialize in massively vectorized operations such as GPUs.

Performance Measurements

Motivation

This section describes a comparison between a filter implementation in Ada and in C. The goal was to verify if DSP algorithms written in Ada language can achieve the same level of performance as the corresponding implementations in C. For this experiment, a simple biquad filter implemented in C language using fixed-point arithmetic was compared to the implementation of the same filter in Ada language.

Filter

A biquad filter has the following form presented in the equation below:

y[n] = a₀ * x[n] + a₁ * x[n − 1]

+ a₂ * x[n − 2] − b₁ * y[n − 1]

− b₂ * y[n − 2]

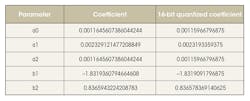
The biquad low-pass filter used for this experiment had the following characteristics indicated by the table below:

These are the filter coefficients, as illustrated by the following table:

Filter implementation

This is the filter implementation in Ada language:

Since the C language doesn’t support fixed-point operations directly, we can emulate them using integer types. This is the corresponding filter implementation:

Optimization of filter implementation

Many DSP implementations written in C employ an optimized version of the fixed-point multiplication. Instead of using an integer division, an arithmetic right shift is used. For the previous filter, the following modification would be applied to the C source code:

In the Ada implementation, developers don’t need to directly change the operations in the filter implementation. Instead, the fixed-point operation can be overloaded. Here’s an example of how this could be implemented for 32-bit fixed-point data types:

This implementation utilizes low-level operations that are very similar to the version in C. Once an overloaded operator for a data type is available, it will be applied in all instances that make use of variables of this type. In this specific example, there’s no need to adapt the filter implementation.

Test application for performance measurements

The remaining part of the implementation, which includes wavefile reading, call to the biquad filter, and clock counting for performance measurements, was completely written in the Ada language. In other words, only the filter implementation was created in two different languages—the test application is the same in both cases. Therefore, we can be assured that variations in performance measurements are only due to the filter implementation.

This is the package specification for the biquad filter:

In the case of linking to the C implementation, a pragma is added to the function declaration:

To minimize the effects of the underlying operating systems, multiprocessor features of the Ada language were used:

Performance measurements

The time spent for each filter called was measured on a PC. To obtain more accurate figures, the same input wavefile was looped 1000 times in the test application.

The compiler (gcc) was set to use the same optimization level (-O3) in all cases. Also, in the case of the Ada implementation, all range checks were deactivated for the filter. For the release version of an application, some checks, especially on the hot spots, can be deactivated after conducting thorough tests.

The performance measurements resulted in an average elapsed time per filter call of 155 ns for the original implementation, and 148 ns for the optimized implementation. In other words, the performance of this DSP algorithm written in Ada language is in the same level as the corresponding implementations in C language. Also, it’s straightforward to optimize operations used in the Ada version, as we’ve just demonstrated.

Conclusions

This article presented an overview of the Ada language and its use in digital-signal-processing applications. We identified that Ada has many features supporting reliable DSP software development, such as strong data types, automatic range checks, overflow checks, and parameter modes.

In addition, the language facilitates DSP software development with its native support for fixed-point data types. Ada offers a great degree of flexibility and abstraction with features such as packages and generics. Moreover, its native support for multitasking with focus on safety makes it easy to convert single-threaded into multithreaded applications.

We were able to successfully port a MPEG-2 Layer-2 decoder implementation originally written in C to the Ada language. As we demonstrated in many of the source-code examples based on the Ada implementation, the use of several features of the Ada language made the porting work in a very straightforward manner. The Ada language and the GNAT compiler made it possible to detect many errors at compilation time, as when using automatic runtime checks. Other key points include:

• The ported implementation in Ada had better source-code readability when compared to the original implementation in C. The most prominent example of improvement in readability is that of fixed-point operations: While the original version in C implemented these operations as function calls, they were replaced by common mathematical operators in the Ada version. Moreover, the associated data types could be mapped to either floating- or fixed-point data types without requiring many changes in the source code. This made the Ada implementation very flexible.
• There were no significant numeric differences in the audio output between the original and ported implementations.
• In terms of robustness, the ported implementation was able to cope with the same set of erroneous input bitstreams as the original implementation. Moreover, the implementation in Ada reached a higher level—it was possible to detect error conditions that went unnoticed in the original implementation in C, such as the use of wrong table indices.

With the GNAT compiler, applications can be written with the same level of performance as the corresponding code in C by removing the checks on the hot spots for the release version. Moreover, operator overloading allows for customizing any operator according to the specific requirements, be it a saturating addition or a simplified (highly optimized) multiplication.

In summary, Ada is a language that offers all of the features and performance needed to write reliable audio applications.

Acknowledgments

The authors thank Claus-Christian Spenger (Dolby) and Quentin Ochem, Richard Kenner, Yannick Moy, Edmond Schonberg, and Eric Botcazou (AdaCore) for their valuable suggestions and remarks.

References

Ada Conformity Assessment Authority. (2012). Ada Reference Manual. ISO/IEC 8652:2012(E) with COR.1:2016. International Organization for Standardization. Retrieved from http://www.ada-auth.org/standards/rm12_w_tc1/RM-Final.pdf.

Ada Rapporteur Group. (2017). New syntax and semantics to facilitate parallelism via Parallel Loops and Parallel Blocks. Retrieved from http://www.ada-auth.org/cgi-bin/cvsweb.cgi/ai12s/ai12-0119-1.txt?rev=1.4.

AdaCore Inc. (2017). Ada Standard and Implementation Defined Restrictions. Retrieved from https://docs.adacore.com/gnat_rm-docs/html/gnat_rm/gnat_rm/standard_and_implementation_defined_restrictions.html.

AdaCore Inc. (2017). AdaCore Case Studies. Retrieved from https://www.adacore.com/industries.

AdaCore Inc. (2017). GPRBuild Documentation. Retrieved from http://docs.adacore.com/gprbuild-docs/html/gprbuild_ug.html.

Barnes, J. (2014). Programming in Ada 2012. Cambridge University Press.

Ben-Ari, M. (2009). Ada for Software Engineers (Second Edition with Ada 2005). Springer.

Brandenburg, K., & Stoll, G. (1994). ISO/MPEG-1 Audio: A Generic Standard for Coding of High-Quality Digital Audio. Journal of the Audio Engineering Society, 42(10), 780–792.

Detlefs, D., Dosser, A., & Zorn, B. (1994). Memory allocation costs in large C and C++ programs. Software: Practice and Experience, 24(6):527–542.

Feldman, M. B. (2014). Who’s Using Ada? Real-World Projects powered by the Ada Programming Language. Retrieved from https://www.seas.gwu.edu/%7Emfeldman/ada-project-summary.html.

Free Software Foundation. (2017). GNAT User’s Guide for Native Platforms. Retrieved from https://gcc.gnu.org/onlinedocs/gnat_ugn/Warning-Message-Control.html.

Gouy, I. (2016). The Computer Language Benchmarks Game. Retrieved from http://benchmarksgame.alioth.debian.org.

Hicks, M., Morrisett, G., Grossman, D., & Jim, T. (2004). Experience with safe manual memory management in cyclone. Proceedings of the 4th International Symposium on Memory Management, ISMM ’04 (pp. 73–84). New York: ACM.

International Organization for Standardization. (1993, August). Information technology - Coding of moving pictures and associated audio for digital storage media at up to about 1,5 Mbit/s - Part 3: Audio. . Geneva, CH: International Organization for Standardization.

Szekeres, L., Payer, M., Wei, T., & Song, D. (2013). SoK: Eternal War in Memory. Proceedings of the 2013 IEEE Symposium on Security and Privacy, SP ’13 (pp. 48–62). IEEE Computer Society.

Taft, T., Moore, B., Pinho, L. M., & Michell, S. (2016). Reduction of parallel computation in the parallel model for Ada. Ada Letters, XXXVI(1):9–24.

Zeigler, S. (1995). Comparing Development Costs of C and Ada. Retrieved from http://archive.adaic.com/intro/ada-vs-c/cada_art.html.