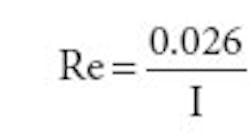No-Load Specification Impacts Power-Supply Performance

When reviewing power-supply specification requirements and supporting design proposals, we often see the minimum load identified as 0 A loading. Although not an issue in and of itself, this no-load requirement significantly degrades the power supply's performance.

One elusive design requirement often called out in power-supply specifications is “no degradation due to bus transients and inrush or outrush current.” Operating a power supply at no load, in most cases, will not cause catastrophic failure; however, overvoltage or stability-related issues, which are caused by the no-load condition, can result in degradation. The extent of the damage is often difficult to quantify.

The no-load requirement generally necessitates a significant degradation in the closed-loop performance (line and load step responses, for example) to maintain the overall power-supply stability in the no-load condition. This performance degradation could require larger capacitors, as well as impose higher stresses on power-supply components. This is generally true, regardless of linear or switching regulation and generally independent of the power-supply topology. Alternatively, preload resistors can be added to the design, which degrades efficiency, increases the power supply's operating temperature and, in turn, reduces its reliability.

A mathematical analysis of the underlying relationship between load current and power-supply performance provides a clearer understanding of no-load operation effects. Several examples, both switching and linear, will show the end effects. You can then make a generalization regarding the specification changes that are necessary to tolerate the no-load requirement.

Normally, power-supply specifications include a “minimum load.” Though, without a specification, you cannot discern the minimum load from the total wattage or other performance aspects. In addition, for supplies with multiple outputs, the minimum load requirements for each voltage are usually different.

Linear Regulator

A linear regulator's seemingly benign topology has a gain of approximately unity, independent of converter loading. You can define a very simplistic low-frequency model as a unity gain stage with an output resistance (for bipolar transistors) defined by Shockley's equation. MOSFETs exhibit similar behavior, although their behavior is less predictable because it depends on their specific manufacturing process. To keep the example simple, we'll use the bipolar transistor shown in Fig. 1.^[1]

Shockley's equation tells us that the intrinsic small signal resistance of a silicon junction is related to the current in the junction as:

This small signal resistance (Re) is in series with the physical resistance of the junction. In this simplified case, we are using a TIP33 n-p-n transistor, which has a physical emitter resistance of approximately 0.25 Ω. Thus, we can calculate the pole created by the transistor resistance and the output capacitor. To further simplify our example, we will use a ceramic output capacitor so we can ignore its ESR effects:

To set the zero frequency for stable performance, fix the maximum bandwidth (arbitrarily) at approximately 100 kHz:

Round off the gain to 1.8 to allow use of a standard resistor value. Then, calculate the integrator capacitor for each of the operating currents:

Figs. 2, 3 and 4 show the step-load simulation results for the circuit in Fig. 1. As we reduce the minimum load current, the resulting response time of the output increases. Therefore, there is a direct relationship between the recovery time of the output and the minimum load current requirement. External load capacitance exacerbates this issue. You see this in the C_OUT term in the numerator of the equation used to calculate the integrating capacitor, so that a requirement for additional capacitance would necessitate a longer response time for stable performance. As discussed earlier, MOSFETs exhibit similar characteristics, though to a larger degree and with less predictability, unless high fidelity models are available.

Buck Regulator

The second example is a nonsynchronous rectified buck switching regulator. Fig. 5 shows the SPICE model of the regulator and Fig. 6 is a state-space average model.^[2] This topology is very common for nonisolated regulator requirements. Many of the newer regulator devices are synchronous, which is exempt from the light load issue. However, there also is a popular control referred to as diode emulation mode, which is not exempt from the light load issue.

The definition of critical load current is the operating load current at which the output inductor current is greater than zero. At or above the critical current the voltage gain of the pulse-width modulation stage is constant (with respect to load current). Its definition is:

The duty cycle in voltage mode control is defined in terms of the peak-to-peak ramp voltage, V_RAMP, and the control voltage, which is the output of the error amplifier. The definition of this relationship is:

Substituting for duty:

Then, solving for the gain, which is the derivative of V_OUT with respect to V_C:

There is no load current term in this equation, and so the modulator gain is independent of the operating load current if the load current is greater than the critical current. Below the critical current, the gain is reduced as a function of the load current. As the load current decreases, the bandwidth decreases. At some operating current, the bandwidth of the regulator may fall below the zero in the compensation network, which would significantly degrade its stability.

Fig. 7 is the bode response of the circuit in Fig. 5, and Fig. 8 shows its step-load simulation results. According to these results, at very low load currents the phase margin falls to 30 degrees, causing ringing in response to the step load. It also is evident that the ringing is much more severe when switching to 5 mA than it is when switching to 50 mA. This clearly shows the relationship between stability and load current.

Because most specifications require a minimum phase margin of 45 degrees (our 30 degrees is nominal and not worst case), some corrective action would be required. One possibility would be to add an internal preload to assure the regulator load will never be below 50 mA, though this degrades the regulator's efficiency. Another choice is to increase the value of the integrating capacitor (C2) to reduce the zero location below the crossover frequency. This will improve the phase margin and reduce the resulting ringing, although it will degrade recovery time and step-load excursions as shown in Fig. 8.

Regardless of the incorporated solution, the regulator's performance had to suffer so it could accommodate the very low-load or no-load condition. Consider these ramifications carefully when developing a power supply's specification, design and test procedures.

References

1. “SPICE Uncovers Regulator Stability Problems,” PEIN August 1998, www.aeng.com/pub.asp.

2. Sandler, Steven M. Switch-Mode Power Supply Simulation with PSPICE and SPICE 3, Chapter 4, McGraw-Hill, 2006, ISBN 0-07-146326-7.

3. Power IC Model Library for PSPICE documentation, AEi Systems, 2005.