Members can download this article in PDF format.
What you’ll learn:
- What are Stackelberg games and how do they apply to power systems?
- What is an IEEE 9 bus?
The Stackelberg game approach is defined as a strategic game in economics. It models a competition between a leader and a follower. This article highlights some Stackelberg games for power systems.
Our first game will be to create a Stackelberg game for voltage stability in cybersecurity power systems.1 This game will have an attacker and a defender in such a power system. Investment resources will be strategically allocated so that we optimize the players’ performance objectives while also saving costs. It was demonstrated that the voltage stability will be maintained unless a defender’s security budget is far lower than an attacker’s budget.
The IEEE 9 Bus System
An IEEE 9 bus system5 is defined as a three-phase power-system network that’s used as a benchmark test case for power-system control and stability. The system will consist of three generator subsystems, each comprising a synchronous machine and associated automatic voltage regulator (AVR), exciter, power system stabilizer (PSS), governor, and prime mover. The system also includes loads and transmission lines.
Researchers use the IEEE 9 bus system to implement innovative ideas and concepts in the field of power systems.2 MATLAB and Simulink provide an example of how to model the IEEE 9-bus system. The example is based on the IEEE benchmark test case and includes a load-flow analysis for the model.1
To distribute generated power economically, amidst a large system amount as well as a minimum cost, a faster divergent technique known as economic load dispatch (ELD) is introduced. This basic tool pertains to the optimum generation scheduling of available power, in an interconnected power system, that’s able to reduce the cost of generation depending on proper system constraints.
The most favorable power flow of the modified IEEE 9 bus system is based on ELD optimization that uses MATPOWER as simulation software.
Engaging in a Stackelberg Game
This is a game between an attacker and a defender of a power system. Here’s how to proceed:
The attacker tries to change the load setpoints of the power system intelligently and clandestinely to reduce the voltage stability margin of the grid. This action will drive the entire system toward a voltage collapse.1,2,7,8
Next, the defender, or the system operator, will attempt to take care of this reduction by retuning the reactive power injection to the electrical grid via the switching on of control devices—for example, a bank of shunt capacitors.
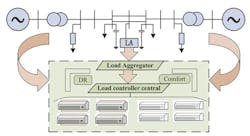
Another game can consist of an online multi-player Stackelberg game control framework. It will attain frequency control of multi-area, smart-grid, power systems with such uncertainties as load, line loss, and renewable energy (see figure).
This multi-player, game-based control framework can achieve a balance between control cost and control performance. The improved integral reinforcement learning (IRL) iterative algorithm incorporates line-loss uncertainty analysis. It’s quite effective in solving the game policy equilibrium solution with wide flexibility in the presence of unknown system dynamics.
The experiment and simulation results show that the proposed algorithm can converge to the equilibrium point in addition to the computational speed meeting the real-time demand.
Finally, a third Stackelberg game variation studies a mixed H2/H∞ control3 problem for nonlinear closed-loop Stackelberg games by means of an adaptive dynamic programming (ADP) technology.
An ADP-based robust control approach can deal with multi-player Stackelberg games.
Adaptive Dynamic Programming
Today’s industrial systems are fast becoming complicated and reaching a large scale. This leads to the requirement of multiple controllers that can execute the variable tasks, such as communication network systems, intelligent transportation systems, microgrid systems, and so on.
Game theory has become a compelling method to cope with the best control of multi-player systems.6,7 Within the context of game theory, each controller is considered as a player. Games are typically divided into two categories:
- Cooperative games: All players work cooperatively to complete control tasks by increasing their benefits.
- Non-cooperative games: All players work cooperatively to complete control tasks by increasing their benefits. This is different from cooperative games. Players in non-cooperative games choose individual decision-making ability.
From the perspective of conflict or cooperation among the players, they can be further divided into zero-sum and non-zero-sum games. The nonlinear Hamilton-Jacobi-Bellman (HJB) equation, which is intractable to acquire the analytic solution, is needed to solve in games due to the “curse of dimensionality.”
H∞ control studies the anti-interference ability of a system. The properly designed controller will be able to attenuate the suppression coefficient of adjusting error and any external disturbance to a set minimum level. The suppression coefficient of adjusting error, in H∞ control, is a measure of the controller’s ability to attenuate the effect of external disturbances on the system.
A robust control ADP-based approach will provide one of the applicable approximating technologies. An algorithm based on the ADP algorithm approximates and solves the nonlinear Hamilton-Jacobi-Bellman equations (HJB).
The common concept of solutions in differential games is the Nash equilibrium, in which the decision hierarchy of each player is the same, and all of the players are assumed to be rational (i.e., only pursue their own optimal strategy). Meanwhile, there’s no order for the announced decisions. Unlike the Nash equilibrium, a hierarchical relationship exists between leaders and followers in Stackelberg games.
References
1. “A Stackelberg Security Investment Game for Voltage Stability of Power Systems,” Lu An, Aranya Chakrabortty, and Alexandra Duel-Hallen, 2020 59th IEEE Conference on Decision and Control (CDC) Jeju Island, Republic of Korea, December 14-18, 2020.
2. “Multiplayer Stackelberg Game-Based Intelligent Frequency Control of Power System With Line Loss Uncertainty,” Xin Tong, Dazhong Ma, Senior Member, IEEE, Rui Wang, Member, IEEE, Qiuye Sun, Senior Member, IEEE, and Huaguang Zhang, Fellow, IEEE, IEEE Transactions on Automation Science and Engineering.
3. “Mixed H2/H∞ Control for Nonlinear Closed-Loop Stackelberg Games With Application to Power Systems, Zhongyang Ming, Huaguang Zhang, Fellow, IEEE, Yushuai Li, Member, IEEE, and Yuling Liang, IEEE Transactions on Automation Science and Engineering, Vol. 21, No. 1, January 2024.
4. Management Science and Engineering (MS&E) 246: Lecture 7 Stackelberg games, Stanford, Ramesh Johari, 2007.
5. “Optimum Power Flow of Modified IEEE 9 Bus System Using ELD Optimization Method,” Anik Nath, A K M Abdur Rahman Chowdhury, Nur Mohammad, 2019 IEEE International Conference on Power, Electrical, and Electronics and Industrial Applications (PEEIACON), Nov. 29-Dec. 1, 2019, Dhaka, Bangladesh.
6. “Adaptive dynamic programming approach for Stackelberg game-based fault-tolerant control,” Yuhang Xu, Bin Jiang, Yizhen Meng, 2023 6th International Symposium on Autonomous Systems (ISAS), IEEE 2023.
7. “Multi-Player Robust Control of Stackelberg Games via Adaptive Dynamic Programming,” Yongwei Zhang, Shunchao Zhang, Bo Zhao, Derong Liu, 2022 IEEE 11th Data Driven Control and Learning Systems Conference (DDCLS), August 5-7, 2022, Emeishan, China, IEEE 2022.
8. MS&E 246: Lecture 7 Stackelberg games, Ramesh Johari.
