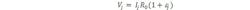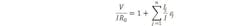Current shunt power coefficient determination

Based on a Fluke Calibration paper¹

Current often is derived from the voltage drop measured across a shunt of known value. However, as the paper states, “It is common practice for current shunts to be calibrated at a single current level and then used over a wide range of currents. The power coefficient (PC) of the shunt can contribute significant error to the measurement process. Often the power coefficient is ignored either through lack of awareness or because it is specified to be acceptably small. For many shunts, however, the power coefficient is far from insignificant and an accurate characterization can provide a set of power coefficient corrections that can significantly reduce measurement uncertainty.”

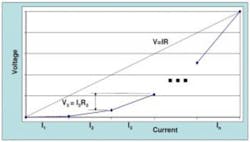
Given the obvious advantage provided by including the effect of a shunt’s PC, the problem then is to devise a means of measuring it. Several straightforward methods that require the use of a calibrated standard shunt are discussed in the paper. For example, connecting the unknown (UUT) and standard shunts in series, as shown in Figure 1, ensures that the same current passes through both. However, the currents I₁ through I₄, although small, are not zero. These bias currents must be low enough to have an insignificant effect on the measurement to the accuracy level required.

Figure 1. Straightforward comparison method

Direct comparison at different current levels is useful, but, as the paper’s authors noted, although the PCs of two shunts compared to within 2 or 3 µΩ/Ω between 10 A and 20 A, both shunts had about a 12-µΩ/Ω shift in value over that current range. Most likely, this was caused by the manganin alloy wire used in the shunt construction. Manganin exhibits a zero temperature coefficient (TC) at room temperature and a negative TC at both lower and higher temperatures.

New Approach

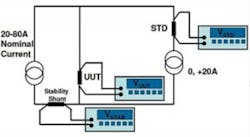
A new test setup devised both to provide accurate PC measurement as well as minimize the effects of reference shunt uncertainties is shown in Figure 2. Two current sources are used, one that changes its output in 20-A steps from 20 A to 80 A and the other switchable from zero to +20 A or -20 A. For each 20-A step in the first source, the other source is stepped through -20 A, zero, and +20 A, with voltage measurements across the UUT taken for each combination of currents. This method creates a series of readings taken “symmetrically in time about the UUT DMM readings.” The readings can be averaged to eliminate most of the effect of any drift in the values of the shunts.

Figure 2. New segmented current approach

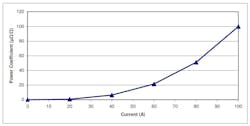
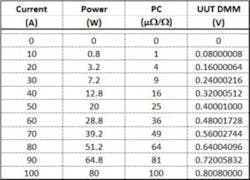
To demonstrate the procedure, the PC of a hypothetical 0.008-Ω 100-A UUT was evaluated. The STD shunt has a value of 0.01 Ω and the Stability shunt 0.001 W. It is assumed that the UUT PC is linear with power as shown in Table 1, with a value of 0.01 *I² µΩ/Ω.

Table 1. Ideal UUT voltages for postulated square-law PC behavior

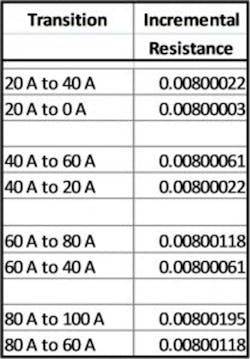
The entries in Table 2 were calculated using the nominal STAB and STD shunt values. Analysis of the data provides incremental values of UUT voltage vs. current. Dividing incremental voltage by incremental current gives the value of the incremental resistance, shown in Table 3. Figure 3 further defines the relationships among these quantities.

where:

V₁, V₂ are incremental voltages caused by changes in current

I is the total current

e is the PC at the total current I: e_n is the PC at current I_n

R₀ is the UUT shunt resistance value at low current; negligible PC

Table 2. UUT voltages resulting from simulated series of test steps
(Click image to enlarge)

Table 3. Incremental resistances derived from Table 2

Figure 3. Incremental voltage and current relationship
(Click image to enlarge)

Each segment can be expressed as

Up to this point, no approximations have been made, but to solve the equations, the values of the STD and Stability shunts must be accurately known. If instead, R₀ is assumed to be equal to the slope of the first segment, or R₀ = V₁/I₁, then the analysis can progress without an accurate knowledge of the STD and Stability shunt values. The paper suggests using several current increments. “If we use five approximately equal current segments and if the power coefficient is proportional to the power dissipated in the shunt (proportional to the square of the applied current), the power at 20% of the current will be 4% of the power at full scale. Thus, after-the-fact we can apply 4% of the total power coefficient as the power coefficient for the first segment. This calculation could be iterated for greater accuracy but that is seldom necessary. The initial calculation can be used to test the hypothesis that the power coefficient is proportional to power. If it is not a linear function of power, the data can be fit to a curve before calculating how much power coefficient to apply to the first segment.”

Working through the math using the R₀ = V₁/I₁ approximation

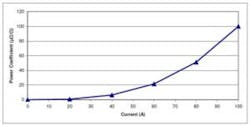
Table 4 demonstrates that the measurement method returned the expected PC values for the UUT in this experiment: it followed a current-squared curve as shown in Figure 4. Table 4 includes the post-analysis 4% correction—the 3.8 value for e₁is equal to 4% of 96—the total uncorrected power coefficient. Dividing the sum by 5 in the third column from the right hand end accounts for each I_j being only 1/5 of the total I.