Three Key PHY Performance Metrics for a JESD204B Transmitter
With the increased adoption of the JESD204 interface in data converters, it’s become necessary to devote more attention to the performance and optimization of the digital interface—the focus must not be only on the data-converter performance.
The first two versions of the standard, JESD204 in 2006 and JESD204A in 2008, specified data rates of 3.125 Gb/s. The latest revision, JESD204B released in 2011, lists three speed grades with the maximum data rate of 12.5 Gb/s.
These three speed grades are governed by three different electrical interface specifications formulated by the Optical Internetworking Forum (OIF). For data rates up to 3.125 Gb/s, OIF-Sx5-01.0 details the interface specifications; the CEI-6G-SR and CEI-11G-SR detail the specs for data rates up to 6.375 Gb/s and 12.5 Gb/s, respectively. The high-speed data rates require that more scrutiny be given to the design and performance of the high-speed CML drivers, receivers, and interconnect network that make up the physical interface (PHY) of the JESD204B interface.
Evaluating the performance of the PHY for a JESD204B transmitter involves evaluation of several performance metrics. These include common-mode voltage, differential peak-to-peak voltage, differential impedance, differential output return loss, common-mode return loss, transmitter short-circuit current, eye diagram mask, and jitter.
This article will focus on three key performance metrics that are typically used to evaluate the quality of the transmitted signal: the eye diagram, the bathtub plot, and the histogram plot. These measurements are made from the perspective of the receiver, as that’s where the signal must be properly decoded.
The eye diagram overlays multiple acquisitions of the output data transitions to create a plot that can give many indications of the link quality. This plot can be used to observe many characteristics of the JESD204B physical interface, such as impedance discontinuities and improper terminations. This is just one way to evaluate the physical layer.
The bathtub plot and the histogram plot are two other important performance metrics used to evaluate the quality of the JESD204B link. The bathtub plot gives a visual representation of the bit error rate (BER) for a given eye-width opening, measured in terms of the unit interval (UI). The UI is the specified time given in the physical-layer specifications for JESD204B that gives the amount of time between data transitions. The third measurement is the histogram plot, which gives the distribution of the measured UI variation.
The measurement is also an indication of the amount of jitter present in the measured signal. This plot, along with the eye diagram and the bathtub plot, can be used to gauge the overall performance of the physical layer of the JESD204B interface. A JESD204B transmitter with a 5.0 Gb/s output data rate is presented. The performance for a transmitter of this data rate is detailed by the OIF CEI-6G-SR specification.
The Eye Diagram
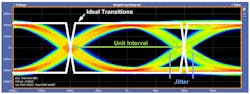
Figure 1 shows an eye diagram for a JESD204B transmitter with a 5.0-Gb/s data rate. The ideal waveform is overlaid on a measured waveform. Ideally, the transitions would be almost instantaneous with no overshoot or undershoot and without any ringing. In addition, the cross points that determine the UI would be without jitter.
As can be seen from Figure 1, in a real system, ideal waveforms aren’t possible to achieve due to nonideal transmission media, which has loss and terminations that aren’t matched exactly. The eye diagram shown is a measurement made at the receiver in a JESD204B system. The signal has passed through a connector and approximately 20 cm of differential transmission lines before making it to the measurement point.
This eye diagram indicates a reasonable impedance match between the transmitter and receiver and a good transmission media with no large impedance discontinuities. It does exhibit an amount of jitter, but not in excess of the specifications for the JESD204 interface. The eye diagram doesn’t exhibit any overshoot; however, it does have a slight amount of undershoot on the rising edges due to the slowing of the signal as it passes through the transmission media. This is to be expected, though, after passing through the connector and the 20 cm of differential transmission lines. The mean UI looks to match the expected UI of approximately 200 ps with the signal having a small amount of jitter.
Overall, this eye diagram presents a good signal to the receiver, which should have no trouble recovering the embedded data clock and properly decoding the data.
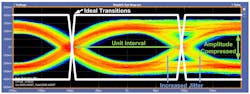
The eye diagram presented in Figure 2 is measured with the same transmission media used in the measurement for Figure 1, with the exception that the termination impedance is incorrect. The effects can be seen in the increased amount of jitter present in the signal at the crossing points, as well as in the nontransition areas.
The overall amplitude is compressed in many of the data acquisitions resulting in an eye diagram that is beginning to close. The degradation will cause an increase in the BER at the receiver and could possibly result in the loss of the JESD204B link at the receiver if the eye closes beyond what the receiver can tolerate.
The eye diagram shown in Figure 3 presents another case of a nonideal transmission of data. Here, an impedance discontinuity is presented at a point midway between the transmitter and the receiver (in this case, an oscilloscope). As can be seen by the degraded performance in the plot, the eye opening is closing, meaning that the area inside the transition points is getting smaller.
The rising edges and falling edges of the data severely degraded due to the reflections of the impedance discontinuity on the transmission line. The impedance discontinuity also contributes to an increase in the amount of jitter seen at the data transition points. Once the eye closes beyond the limits of the receiver’s capability to decode the data stream, the data link will be lost. In the case of Figure 3, it’s likely that many receivers would be unable to decode the data stream.
The Bathtub Plot
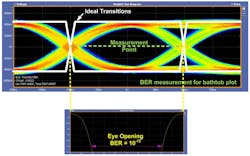
Like the eye diagram, the bathtub plot also provides useful insight into the quality of the serial data transmission on a JESD204B data link. The bathtub plot is a measurement of the BER as a function of the sampling point as it moves across the eye diagram in time.
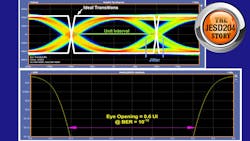
The bathtub plot is generated by moving the sampling point across the eye diagram and measuring the resultant BER at each point. The closer the sampling point is to the center of the eye, the BER decreases (Fig. 4). As the sampling point moves closer to the transition points of the eye diagram, the BER increases. The distance between the two slopes of the bathtub plot at a given BER gives the eye opening at the specified BER (10-12 in this case).
The bathtub plot also provides information on the total-jitter (Tj) components present in the signal. As Figure 5 shows, when the measurement point is at or near the transition points, it’s relatively flat and the main jitter component is deterministic jitter.
Like the eye-diagram measurements, the bathtub plots are from measurements on a JESD204B 5.0-Gb/s transmitter measured at the receiver after passing through a connector and approximately 20 cm of transmission line. As the measurement point moves closer to the middle of the eye opening, the primary jitter mechanism is random jitter. Random jitter is the result of numerous processes that are typically small in magnitude. Typical sources would include thermal noise, variations in trace width, shot noise, etc.
The probability density function (PDF) of random jitter usually follows a Gaussian distribution. On the other hand, deterministic jitter results from a small number of processes that may have large magnitudes and may not be independent. The PDF of deterministic jitter is bounded and maintains a well-defined peak-to-peak value. It can have varying shapes and is typically not Gaussian.
An expanded view of the bathtub plot discussed in Figure 4 is given in Figure 6. This represents an eye opening of approximately 0.6 UI at the receiver for a 5.0-Gb/s serial data transmission with a BER of 10-12. It’s important to note that the bathtub plot like that in Figure 6 is an extrapolated measurement. The oscilloscope used to capture the data takes a set of measurements and extrapolates the bathtub plot. If one were to use a bit-error-rate tester (BERT) and acquire enough measurements to build the bathtub plot, it could take hours or even days, even with the high-speed operation of today’s test equipment.
Just as shown in the eye diagram, an improper termination or impedance discontinuity in the system can be seen in the bathtub plot. In contrast to Figure 6, the bathtub plots in Figures 7 and 8 exhibit much shallower slopes on each side. The eye opening for a BER of 10-12 is only 0.5 UI in both cases, which is more than 10% less than the 0.6 UI for the good condition.
The improper termination and impedance discontinuity contribute a large amount of random jitter to the system. This is evidenced by the decreasing slope on each side of the bathtub plot along with the decreased eye opening at a BER of 10-12. There’s also a small increase in the deterministic jitter. This is evidenced again by the decreasing slope near the edges of the bathtub plot.
The Histogram Plot
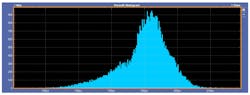
A third useful measurement is the histogram plot. This plot shows the distribution of the measured periods between transition points in the data transmission. As with the eye-diagram and bathtub-plot measurements, the histogram plots are from measurements on a JESD204B 5.0-Gb/s transmitter measured at the receiver after passing through a connector and approximately 20 cm of transmission line.
Figure 9 shows a histogram for a relatively good-performing system at 5.0 Gb/s. The histogram shows a mostly Gaussian-type distribution with periods measured between 185 and 210 ps. The expected period for a 5.0-Gb/s signal should be 200 ps, which means the distribution is spread about −7.5% to +5% around its expected value.
When an improper termination is introduced (Fig. 10), the distribution becomes wider and now varies between 170 and 220 ps. This increases the percentage of variation from −15% to +10%, which is double that of the measurement presented in Figure 9. These plots show that mostly random jitter is present in the signal since they have a mostly Gaussian-like shape. However, the shape isn’t exactly Gaussian in nature, which indicates there’s at least a small amount of deterministic jitter, too.
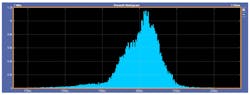
The histogram in Figure 11 indicates the results of having an impedance discontinuity along the transmission line. The shape of the distribution isn’t Gaussian-like at all and has developed a small secondary hump. The mean value of the measured period is also skewed. Unlike the plots in Figure 9 and 10, the mean is no longer 200 ps and has shifted to about 204 ps. The more bimodal distribution indicates that there’s more deterministic jitter in the system. This is due to the impedance discontinuity present on the transmission lines and the predictable impacts it has on the system.
The range of values measured for the period is again increased, although not as much as in the case of improper termination. Here, the range is from 175 up to 215 ps, which is approximately −12.5% to +7.5% of the expected period. The range isn’t as large, but again, the distribution is more bimodal in nature.
Conclusion
It’s important to maintain good design practices to properly terminate the system and avoid impedance discontinuities in the transmission media. These have appreciable negative effects on the data transmission and can result in a faulty data link between the JESD204B transmitter and receiver. Employing techniques to avoid these issues will help to ensure a properly working system.
Jonathan Harris is a product applications engineer in the high speed converter group at Analog Devices.
References
JEDEC Standard JESD204B. JEDEC Solid State Technology Association, July 2011.
“Application Note 5989-5718EN. Using Clock Jitter Analysis to Reduce BER in Serial Data Applications.” Keysight Technologies, July 2014.
“Application Note 5988-9109EN. Measuring in Digital Systems.” Agilent Technologies, June 2003.
About the Author
Jonathan Harris
Applications Engineer, Analog Devices Inc.
Jonathan Harris is a product applications engineer in the High Speed Converter Group at Analog Devices (Greensboro, N.C.). He has over seven years of experience as an applications engineer, supporting products in the RF industry. Jonathan received his MSEE from Auburn University and his BSEE from UNC-Charlotte. In his spare time, he enjoys mobile audio, nitro RC, college football, and spending time with his two children.