Members can download this article in PDF format.
What you’ll learn:
- How data representation is impacted by hardware updates.
- How to use Ada representation clauses to create portable specifications for data representation.
- How to use GNAT’s Scalar_Storage_Order feature to write endianness-agnostic code.
Hopefully, the software you pour your time and effort into will be around to make the world a better place for a long time. But will today’s hardware be sufficient to support future features and requirements? The breakneck pace at which new hardware, with increased resources, comes to market provides some relief for worries. But what if it also results in the obsolescence of your existing hardware? Can your codebase gracefully migrate to new hardware (i.e., can you recompile the source code and expect the correct behavior) when the time for an update arrives?
One issue that arises is the explicit use of non-portable constructs in your programming language; for example, features that are implementation-dependent or have unspecified or undefined behavior. This is a well-studied area, and the standards for languages like C, C++, and Ada identify and characterize all of the features whose semantics can exhibit such behavior.
More subtly, your code may contain implicit assumptions about the underlying machine architecture (bit length, word size, endianness, etc.), and your code could break when compiled for a new hardware target if those assumptions are no longer correct. A commonly affected area of your software will be its external interfaces. Communication protocols typically prescribe the format of data and messages on the communication link in a manner that’s independent of the processor architectures of the endpoints. Memory-mapped external registers are another form of communication where formats are prescribed.
Consider the concrete example of IP packets that are defined in terms of a big-endian data format. Suppose an existing system is big-endian and has the requirement of transmitting an unsigned 32-bit integer over the network. If the existing codebase’s implementation assumes that it’s running on a big-endian machine, one could simply provide the address of a 32-bit unsigned integer primitive as a byte buffer to send directly to the network.
If the number to transmit has the value 0xDEADBEEF, the buffer’s bytes in memory (in order of increasing addresses) will contain 0xDE 0xAD 0xBE 0xEF. Unfortunately, the same code will compile and run on a little-endian machine, but the buffer’s byte contents in memory would be 0xEF 0xBE 0xAD 0xDE, which will be interpreted as a totally different value (0xEFBEADDE) by the receiver!
To create truly portable code, so that the headaches of such hardware updates are a thing of the past, you need to have the tools to allow you to precisely specify how your data is represented in memory when dealing with external interfaces.
The Ada Record Representation Clause
One area in which Ada excels is that the language was designed specifically to solve the problems faced by long-lived embedded projects, which means portability is a primary concern. To achieve (among other benefits) improved portability, Ada has rich specification semantics that give the programmer the tools to precisely control how data is represented in memory, down to the bit!
This feature of the Ada language is known as the record representation clause. To understand this feature, we’ll quickly introduce the concepts of a machine scalar and storage element. Simply put, a storage element is the smallest amount of addressable memory (typically a byte) and a machine scalar is an integer multiple of storage elements that can be efficiently loaded, stored, or operated on by the hardware.
The exact set of machine scalars is implementation-defined and typically includes 8-, 16-, 32- and 64-bit values. The record representation clause allows the programmer to precisely control which bits in a machine scalar will store the fields of a heterogeneous data type (known as a record in Ada or a struct in C/C++).
I’m a fan of learning by example, so let’s create and analyze an Ada specification for a data type used to store calendar dates:
subtype Yr_Type is Natural range 0 .. 127; subtype Mo_Type is Natural range 1 .. 12; subtype Da_Type is Natural range 1 .. 31; type Date_Type is record Years_Since_1980 : Yr_Type; Month : Mo_Type; Day_Of_Month : Da_Type; end record; for Date_Type use record Years_Since_1980 at 0 range 0 .. 6; Month at 0 range 7 .. 10; Day_Of_Month at 0 range 11 .. 15; end record;
In Ada idiomatic fashion, we have declared subtypes of the natural numbers to define valid ranges for Yr_Type, Mo_Type, and Da_Type. The compiler will automatically insert run-time code to ensure no invalid values will be assigned. These types are then used to define the record type Date_Type.
Finally, a representation clause is introduced using the use record keywords to specify that the Years_Since_1980 field be located at bits 0 through 6 of the 0-th machine scalar, the Month field be located at bits 7 through 10 of the 0-th machine scalar, and that the Day_Of_Month field be located at bits 11 through 15 in the 0-th machine scalar. Notice that the machine scalar needn’t be explicitly specified (in contrast to C/C++ bitfields)—the Ada compiler takes responsibility for making the proper selection.
At this point, those of you that have had the pleasure of dealing with data-representation issues are probably asking questions such as: “Is the least significant bit (LSB) the 0-th bit?” “How are storage elements ordered in memory?”
Dealing with Bit Ordering and Endianness
The answers to these questions are particularly important when retargeting an application from legacy hardware of a given endianness to another platform with different endianness. If any data was stored in memory or persistent storage by the legacy system, or if interoperability with other subsystems needs to be preserved, all data structures must have precisely the same representation on the two platforms. Where portability is a concern, attributes must be used to override the implementation-defined native bit ordering and endianness. Let’s focus on the specific case of a target with an x86_64 architecture.
It’s important to keep in mind that bit offsets for a component in a record representation clause are always relative to some machine scalar. In general, the component value is extracted and set using shift and mask operations.
To find out which machine scalar a given component belongs to, you must first identify the set of components that share the same machine-scalar offset. In our example, this would be all three components since all are specified with an offset of 0. The compiler determines the machine scalar used by selecting the smallest machine scalar whose bitlength is greater than the greatest bit offset specified for any field in the record’s representation clause.
In this example, the x86_64 architecture provides a two-byte integer machine scalar that the compiler will use for this data type. (You can specify alignment requirements separately in case the type’s instances need an alignment stricter than what’s implied by the machine-scalar size. This is an interesting topic, and handled nicely in Ada, but is outside the scope of this article.)
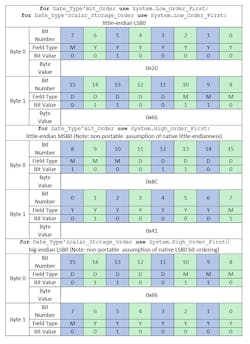
Bit ordering refers to the numbering of bits in a machine scalar, and endianness refers to the ordering of the storage elements from which the machine scalar is composed. These orderings are a property of the target hardware and can be independent.
The machine scalar is a logical entity with two important properties:
- The most significant bit is always the left-most bit.
- The most significant byte is always the left-most byte.
The key to understanding bit ordering is to know that the bit significance property holds for any range of bits in the machine scalar regardless of how they’re ordered (numbered). Bits are numbered in ascending order starting from 0 and the bit ordering simply defines the number used to refer to a bit in the machine scalar. Storage element ordering (endianness) is similarly just an ordering (numbering) of the bytes of a machine scalar and manifests itself as the machine placing bytes into memory in ascending order.
Table 1 illustrates the difference between the bit ordering where the most significant bit is 0 (abbreviated MSB0) and the bit ordering where the least significant bit is 0 (abbreviated LSB0). It also illustrates the difference in storage element ordering between little-endian and big-endian encodings. Note that the values of the machine scalar’s bits are the same and don’t change based on the orderings.
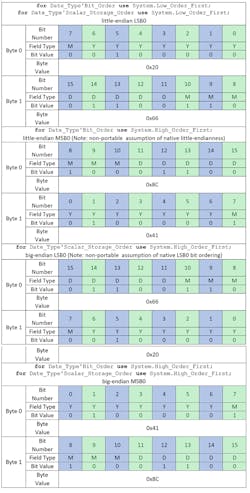
Things get interesting when we want to represent values in specific ranges of bits in the machine scalar; for example, in our Date_Type record above. Suppose we want to store “December 12th, 2012” in an object of Date_Type. The Years_Since_1980 field will have a value of 32, the Mo_Type field will have a value of 12, and the Day_Of_Month field will also have a value of 12. The bits used to store each field in the machine scalar will be different depending on the bit order specified (Table 2).
The key observation is that only the range of bits used to represent each field have changed but the bit values used to encode each field, from left to right in each bit range, remain the same. In this sense, specifying the bit ordering controls which bits of the machine scalar are used to encode each field. Note that we still do not know the data layout (i.e., the order of bytes) in memory—this still depends on the target endianness.
It’s precisely in order to overcome this limitation that the Scalar_Storage_Order attribute was introduced in the GNAT Ada, C, and C++ compilers. The effect of this attribute is to override the order of storage elements in machine scalars for a given record type, i.e., to control the endianness. If both the endianness and bit ordering are known, the actual memory representation of the data is fully determined.
There are four possible combinations of bit ordering and endianness, but GNAT restricts the possibilities to Little Endian LSB0 and Big Endian MSB0. These two combinations provide enough flexibility to allow the programmer to have full control of data layout in memory. The more exotic combinations of little-endian MSB0 and big-endian LSB0 can still exist, but require assumptions on the target architecture (and are thus non portable!).
The x86_64 architecture uses little-endian and LSB0 natively. Specifying the Date_Type’s Bit_Order and Scalar_Storage_Order attributes with Ada aspects can yield the memory representations shown in Table 3 on this target.
Existing code for a big-endian system can thus be ported to a little-endian system without any fuss, and without any change of data representation—just add appropriate attribute definitions on the relevant record type declarations. After these attributes have been defined on data types whose data representations need to be fully specified, future hardware updates become automatic and painless. This is because the compiler takes the responsibility of generating and inserting runtime code for bit-shifting, bit-masking, and byte-flipping.
One thing to keep in mind is the tradeoff between performance and portability when a data type’s representation specification differs from the native representation. The additional runtime code required to make the code portable may not be appropriate in sections of the code with strong performance requirements. In such a case, rewriting the code for the specific target’s architecture may be unavoidable.
Conclusion
Defining physical data representations in a portable manner is non-trivial, and faulty endianness assumptions are a common source of errors in an application’s external interface, whether it be via memory-mapped registers or communication protocols. If an application’s data can’t be precisely laid out in memory when needed, hardware updates may prove to be unnecessarily costly, time-consuming, and risky.
This article demonstrates how a data type’s memory representation can easily be fully specified using the features of the Ada language and GNAT compilers, independent of the endianness of the underlying hardware. This allows the programmer to develop portable, long-lived applications insulated from the risks of hardware migration.
To learn more about Ada, we encourage you to visit the free, online, interactive training site learn.adacore.com.