From the Electronic Design Archives. This article appeared in the November 8, 1990 issue.
Members can download this article in PDF format.
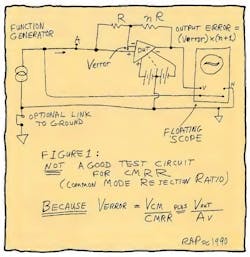
Recently, many people have asked me about how to test op amps for common-mode rejection ratio (CMRR), which is defined as the delta of the offset voltage (Vqs) versus the common-mode voltage (Vcm). The first thing I tell them is how not to measure CMRR (Fig. 1). If you drive a sine wave or triangle wave into point A, it seems like the output error, as seen by a floating scope, will be (N+1) times (Vcm divided by the CMRR).
But that’s not quite true: you will see (N+1) times (the CM error plus the gain error). So, at moderate frequencies where the gain is rolling off and the CMRR is still high, you will see mostly the gain error, and your curve of CMRR vs. frequency will look just as bad as the Bode plot. That's because with this circuit, that's just what you will be seeing!
It turns out that a few op-amp data sheets still exist in which the CMRR curve is stated to be the same as the Bode plot. The National LF400 and LF401 are two examples; next year we will correct those curves to show that the common-mode rejection ratio is actually much higher than the gain at 100 or 1000 Hz.
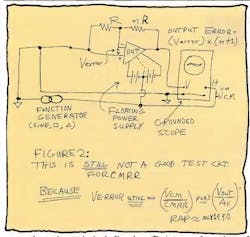
Ah, let's avoid that floating scope. We'll drive the sine wave generator into the mid-point of the power supply, and ground the scope and ground point A (Fig. 2). Then we'll get the true CMRR, because the output won't have to swing. Right? Wrong! The circuit function hasn't changed at all; only the viewpoint of the observer changed. The output does have to swing, referred to any power supply, so this still gives the same wrong answer. You may say that you asked for the CMRR as a function of frequency—but the answer is, in most cases, the curve of gain vs. frequency.
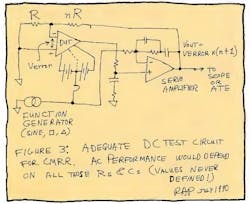
What about, as an alternative, the well-known scheme where an extra servo amplifier closes the loop and doesn't require the op-amp output to do any swinging (Fig. 3). That's okay at dc. So it's adequate for dc testing with automatic test equipment (ATE), for production test, and for stepped dc levels.
And it will give the same answer as my circuit (which I'll discuss a little later) at all low frequencies up to where it doesn't give the same answer. Now what frequency would that be? Nobody knows! Because if you have an op amp with low CMRR, the servo scheme will work accurately up to one frequency. And if you have an op amp with high CMRR, the servo scheme will work accurately only up to a different frequency.
Also, the servo amplifier adds so much gain into the loop that ringing, overshoot, or marginal stability at some mid frequencies is inevitable.
That's much too horrible for me to worry about. I’ll just avoid that by using a circuit which gives very consistent and predictable results.
When I ran an LF356 in the circuit of Figure 1, I got an error of 4 mV pk-pk at 1 kHz—a big fat quadrature error, 90 degrees out of phase with the output (Fig. 4, upper trace). If you think that's the CM error, you might say the CMRR is as low as 5000 at 1 kHz, and falling rapidly as the frequency increases. But the actual CMRR is about 0.2 mV pk-pk (Fig. 4, lower trace). As a result, the CMRR is about 100,000 at 1 kHz or any lower frequency. In addition, the CM error on this unit isn't really linear. As you get near -9 V, the error gets more nonlinear (this is a –9-V to +12-V CM range on a 12-V supply; I chose a +12-V supply so my function generator could overdrive the inputs).
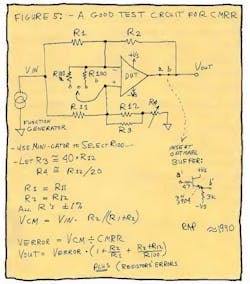
As you can see, this business of CMRR testing isn't trivial. Just how, then, can we test for CMRR and get the right results? Well, there's a darned fine circuit I invented myself about 22 years ago (Fig. 5). It has limitations, but it's the best circuit I've seen. Let's choose R1 = R11 = 1k, R2 = R12 = 10k, and R3 = 200k and R4 = a 500-Ω single-turn carbon pot, or its equivalent.
These values will permit us to set up a more-or-less balanced bridge, with a fine trim for dc balance. In this case, the noise gain is defined as (Rf/ Rin +1), or about 11. Let's put ±11-volt sine wave into the signal input so that the CM voltage is about +10 volts. The output error signal will be about 11 times the error voltage plus some function of the mismatch of all those resistors.
Okay, first connect to the scope's horizontal input, to the vertical input, and operate the scope in cross-plot (X-Y) mode. Trim pot R4 until the output error is very small, or until the slope is nominally flat. We don't know if the CMRR error is balanced out by the resistor error or whatever, but it turns out we don't care. Just observe that the output error, as viewed on a cross-plot scope, is quite small. Now connect in R110a a nice low value, such as 200 Ω. If you sit down and compute it, the noise gain rises from 11 to 111. Namely, the noise gain was (1 + R2/R1), increasing to (1 + R2/R1) plus (R2 + R12)/R100. In this example, that's an increase of 100. So, you're now looking at a change of Vout equal to 100 times the input error voltage, (and that is VCM divided by CMRR).
Of course, it's unlikely for this error voltage to be a linear function of which is why I recommend you look at it with a scope in X-Y mode. Too many people are inclined to make a pretend game that CMRR is constant at all levels and CM error is a linear function of VCM. So they just look at 2 points and assume every other voltage has a linear error; and that's just too silly. Even if you want to use some ATE you will want to look at this error in at least 3 places—maybe even at 4 or 5 voltages.
Another good reason to use a scope in the X-Y mode is so you can use your eyeball to subtract out the noise. You certainly can't use an ac voltmeter to detect the CMRR error. For example, with the waveform of Figure 4 (lower trace), the CM error is fairly stated as 0.2 mV pk-pk, not 0.5 mV pk-pk (as your meter might say if you let it include the noise).
Anyhow, if you have a good amplifier with a CMRR of about 100 dB, the CM error will be about 200 µV pk-pk. When it's magnified by 100, you can easily see an output error of 20 mV pk- pk. If you have a really good unit with CMRR of 120 or 140 dB, you'll want to clip in the R100b such as 20 Ω, and then the delta (noise gain) will be 1000. The noise will be magnified by 1000, but so will the error, and you can see what you need to see. Now I won't get embroiled in the question: Are you trying to see exactly how good the CMRR really is, or just if the CMRR is better than the data sheet value? In either case, this approach is the best way I have seen.
For use with ATE, you don't have to look with a scope; you can use a step or trapezoidal wave and look just at the dc levels at the ends, or the middle, or wherever you need. Note that you needn't trim that resistor network all of the time, nor do you have to trim it perfectly. All you have to know is that when the noise gain changes from a low value to a high value, and the output error changes, the change of the output error is of interest—not really the pk-pk value before or after, but the delta. You don't have to trim the resistor to get the slope perfect, but that's the easy way for the guy working at his bench to see and appreciate the changes.
This is a great circuit to fool around with. When you get it running, you'll want to test every op amp in your area, because it gives you such a neat high-resolution view. It gives you a good feel for what's happening, rather than just hard, cold, dumb numbers. For example, if you see a 22-mV pk-pk output signal that's caused by a 22 µV error signal, you know that the CMRR really is way up near a million, which is much more educational than a cold "119.2 dB" statement.
Besides, you learn rather quickly that the display's slope and curvature are important. Not all amplifiers with the same "119.2 dB" of CMRR are actually the same. Some have a positive slope, some may have a negative slope, and some curve madly, so that if you took a 2-point measurement, the slope would change wildly, depending on which two points you choose (if you increase the amplitude of the input signal, you can also see plainly where severe distortion sets in—that's the extent of the common-mode range).
Limitations: If you set the noise gain as high as 100, then this circuit, of course, will be 3 dB down at (FGBW) divided by 100, so you would only use this up to about 1 kHz on an ordinary 1-MHz op amp, and only up to 100 Hz at a gain of 1000. That's not too bad, really.
To look at CMRR above 1 kHz, you might use R100c ~ 2k to give good results up to 10 kHz. In other words, you have to engineer this circuit a little to know where it gives valid data. You can't avoid the fact that thinking is required. Sorry about that.
For really fast work, I go to a high-speed low-gain version where R1 = R11= 5k, R2 = R22 = 5k, and R100 = 2k or 1k or 0.5k. This works pretty well up to 50 kHz or more, depending on what gain-bandwidth product your amplifier has.
For best results at ac, it's important to avoid stray capacitance of wires or of a real switch at the points where you connect to R100a or R100b. Usually I get excellent results from just grabbing on to the resistor with a mini-gator clip. You can avoid the stray pF that way. If you use a good selector switch, with all of the wires dressed neatly in the air (which is an excellent insulator), you may be able to get decent bandwidth, but you should be aware that you are probably measuring the ac CMRR of your set-up, not of the op amp. Actually, I was discussing this circuit with a colleague, when I realized the best way to make up this 20-Ω resistor is to connect one 10-Ω resistor to each input, and then clip the other ends together with a mini-gator clip up in the air. Balanced strays, and all that.
If you have an op amp with low gain or low gm, you may want to add in a buffer follower at a-b (Fig. 5, again), so the amplifier does not generate a big error due to its low gain. The LM6361 would need a buffer as it only has a gain of 3000 with a load of 10k, and its CMRR is a lot higher than 3000. Altogether, I find this circuit has better resolution and gives less trouble than any other circuit for measuring CM error. And the price is right: a few resistors and a mini-gator clip.
All for now. / Comments invited! / RAP / Robert A. Pease / Engineer
ADDRESS:
Mail Stop C2500A National Semiconductor P.O.Box 58090 Santa Clara, CA 95052-8090
