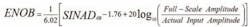Oscilloscopes: Resolving Finer Detail

What you'll learn:

• What are ENOB and SINAD, how to calculate them, and the typical values from several 'scope manufacturers.
• About the many paths used to achieve high resolution in an oscilloscope.
• About the characteristics of higher sensitivity 'scope probes.

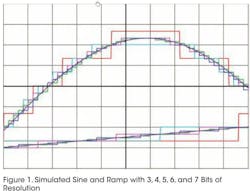
If you use an oscilloscope, you won't have any trouble imagining an instrument with higher resolution. Digital storage oscilloscopes (DSOs) convert analog inputs to digital data with a certain level of precision. Figure 1 shows simulated waveforms with a 16:1 range resolution. The most common resolution is 8 bits or 256 quantization (Q) levels, but high-resolution scopes can have as many as 12 bits (4,096 levels) to 16 bits (65,536 levels) and display fine waveform detail almost as well as an analog scope.

Anomaly hunting is only one activity for which high resolution is important. The large dynamic range associated with high-resolution scopes supports many others. For example, biological research often involves indeterminate signal amplitudes and amounts of offset. With a high-resolution DSO, if the waveform fits vertically within the display graticule, no clipping will occur, and acquired data can be zoomed for closer examination of actual sample values.

Chris Loberg, senior technical marketing manager at Tektronix, cited power supply and mobile platform design as two additional areas that can benefit from the use of high-resolution scopes.

Agilent Technologies' (now Keysight) Ai-Lee Kuan, product marketing engineer, agreed. "The ever-increasing demand for mobile devices and an increased focus on green product development have generated a greater demand for oscilloscopes that can accurately test and characterize these devices," said Kuan. "Noise is often the biggest impediment to getting accurate measurements of the small signals found in applications such as mobile devices and green product characterization where there is need to make low power and high dynamic range voltage and current measurements."

Teledyne LeCroy's Christopher Busso, product marketing manager, took a broader view. He said, "We intended our 12-bit oscilloscopes for any application that can benefit from the ability to observe the finest details of small signals overriding larger-amplitude signals. The same holds true for any applications that require greater accuracy and higher sensitivity."

Both LeCroy and Agilent have a 1-mV/div range, and Rigol Technologies has added a 500-μV/div range to take advantage of low front-end noise.

Further clarifying the role of high-resolution scopes, Pico Technology's Alan Tong, managing director, said, "The market for high-resolution scopes is very different from that of 8-bit scopes. Development of 8-bit scopes has tended to focus on increasing bandwidth and sampling rate to support the measurement of high-speed serial signals. As a result, 8-bit scopes are increasingly digital scopes for measuring digital signals. However, high-resolution scopes are digital scopes for measuring analog signals."

Defining a High-Resolution Scope

Higher resolution by itself seldom is useful. Low noise is a prerequisite to achieving the large dynamic range that users assume a high-resolution scope will provide. Improved accuracy also is important, not just at DC, but throughout the scope's bandwidth. Resolution clearly is distinct from accuracy, but for many users, better accuracy is implied by higher resolution.

Resolution

A full-scale display with 2ⁿ levels has n bits of resolution. The effective number of bits (ENOB) is a much more rigorous definition that includes both noise and distortion:

According to an Analog Devices tutorial, "SIgnal-to-Noise- And-Distortion--SINAD or S/(N + D) is the ratio of the RMS signal amplitude to the mean value of the root-sum-square (RSS) of all other spectral components, including harmonics, but excluding DC. SINAD is a good indication of the overall dynamic performance of an ADC because it includes all components which make up noise and distortion."¹

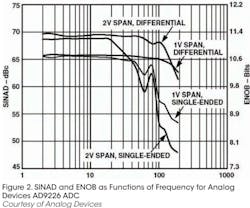
ENOB is the number of bits that an ideal ADC would need to deliver the same measured SINAD as a real ADC with the same input. As shown in Figure 2, ENOB is a function of frequency, and, for the Analog Devices AD9226 12-bit ADC, it's affected by the choice of differential or single-ended drive as well as drive level.

Achieving a high ENOB in a 12-bit DSO is very difficult if high speed also is part of the feature set. If, instead, you want better dynamic performance at a lower speed, Pico Technology's Model 4262 16-bit PicoScope is a good example of what is available. It has a bandwidth of 5 MHz with a spurious-free dynamic range (SFDR) >100 dB and a noise level of only 8.5 μV rms as well as 0.2-dB flatness over the entire bandwidth. DC accuracy is 0.25% of full scale for less sensitive ranges, decreasing to 2% on the 10-mV range.

SFDR is defined as the ratio of the RMS signal to the RMS value of the highest spur whether it's noise or a harmonic. SINAD will be lower than SFDR because it includes the power from all noise and harmonics, not just the largest peak. The signal-to-noise ratio (SNR) excludes harmonics.

LeCroy's 12-bit HDO6000 scope claims a 55-dB SNR. Because SNR does not include harmonics, you have to assume that SINAD will be less than the quoted SNR. This level of performance is not unusual.

An Agilent Technologies application note explained, "ENOB is reduced by all the noise and error sources in the oscilloscope including ADC quantization noise, ADC differential nonlinearity (DNL), ADC integral nonlinearity (INL), thermal noise, shot noise, and input amplifier distortion. You should expect an ENOB specification usually to be much lower than the number-of-bits specification due to these noise and error sources.

For example, an ENOB between 8 bits and 9 bits at high frequency, or equivalently, a SNR between 50 dB and 56 dB, is typical for a 12-bit high-resolution DSO."²

Part of the benefit of using a high-resolution scope is better DC accuracy, LeCroy offering 0.5% and Agilent 1%. However, many applications can be addressed by either a high-resolution scope or a 12- to 16-bit data acquisition (DAQ) system. The DC accuracy of a DAQ system may be 0.1% or 0.05% rather than a scope's typical 1% or 2%. And, DAQ system specifications often include values for ENOB and SFDR.

National Instruments' Model NI PXI/PCI 5922 16- to 24- bit digitizer is a good example of a more fully specified high-resolution DAQ product. Sampling at 1 MS/s with a 100-kHz input signal 1 dB below the 10-V peak-to-peak full scale typically yields a 105-dB SINAD. This is equivalent to an ENOB of 17.3 bits. For a 10-MS/s sampling rate and a 1-MHz signal, the ENOB drops to 14.6 bits. The DC accuracy of this digitizer is 0.05% of input +50-μV offset for the 2-V range or 0.05% +100-μV offset for the 10-V range.

Christian Gindorf, senior product marketing manager for digitizers at the company, said, "NI offers digitizers with up to 24 bits of resolution, as found in the NI PXI-5922... [with] SFDR of up to -114 dBc. Other digitizers like the NI 5761R provide 14-bit resolution and wide analog bandwidth to be used in undersampling applications up to the 4th Nyquist zone."

Noise

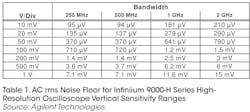
Rather than specify SFDR or ENOB, Agilent quotes the AC RMS noise floor at several input sensitivities and for different bandwidth models in the Infiniium 9000-H Series as shown in Table 1. 

An eight-division peak-to-peak sinewave has an RMS value of 2.83 divisions. For a 250-MHz bandwidth model on the 100-mV range, 0.283/0.00071 = 399. On the 20-mV setting, the ratio is 419. Allowing for some amount of overrange above and below the graticule, these values correspond to about 9 bits of resolution. Without knowing the level of any harmonics that may exist, you can only say that ENOB will be less than 9 bits. and as the table shows, performance degrades further at higher bandwidths.

Reference 1 stated the situation in another way, "...both the LeCroy HRO66Zi, which has a 12-bit ADC, and the Agilent DSO9054H, which has 12 bits of resolution, take advantage of about 10 bits of resolution. The lower 2 bits of resolution are consumed by front-end noise over the entire range of vertical settings."

ZTEC Instruments' ZT4430 13-bit DSO with 250-MHz bandwidth and 500 MS/s sampling rate quotes typical RMS noise with a 50-Ω input as 0.05% of full scale + 75 μV, improving to 0.025% with a 20-MHz band-limiting filter. These noise levels correspond to SNRs of about 56 dB and 63 dB, respectively, or 9 bits to 10 bits. With a 1-MΩ input, the noise increases by 1 mV at full bandwidth and by 500 μV with the 20-MHz filter. On the 1-V full-scale range, the additional noise reduces the SNRs to about 47.5 dB and 53.5 dB, respectively, or 8 bits to 9 bits.

Noise limits performance but also can be manipulated to advantage. As explained in a Tektronix white paper about the spectrum analyzer part of the MDO4000, "The important thing to understand is that the [ADC] noise... is broadband and typically spread uniformly across the bandwidth of the ADC. By using a combination of digital downconversion and DFT to reduce the bandwidth of the data that is actually processed and displayed, the noise floor is lowered, allowing visibility of small signals. This effect is called process gain and improves the SNR as follows:

As an example, for a 10-MHz span and an RBW of 10 kHz (given the MDO4000 sample rate of 10 GS/s), this improves the SNR by roughly 57 dB to about 107 dB."³ Other noise sources reduce this theoretical value somewhat in the actual instrument.

The Many Paths to High Resolution

Basic High-Resolution ADC

The most obvious way to build a high-resolution scope is simply to use a high-resolution ADC together with a suitably low-noise front end. This approach has limited usefulness because many of today's applications mix high- and low-speed requirements. For example, a piece of medical equipment may need to analyze low-level ECG data and download results via Wi-Fi. Bandwidth and sample rate would be a few hundred megahertz at most with this scheme for native resolution greater than 13 bits or 14 bits. Nevertheless, this may be the best way to achieve the highest dynamic range and ENOB performance for applications that need them.

Time Interleaving

Eight-bit scopes often interleave ADCs from multiple channels to increase sampling rate by 2X or 4X. However, individual ADCs in a group of two or four are not identical, and the mismatching among time-interleaved ADCs causes image spurs that quickly degrade performance.

An Analog Dialogue article discussed the application of digital post-processing to optimize the ADC matching. The company's AD12500 (now obsolete) includes four AD9444 14-bit, 80-MS/s ADCs and all the auxiliary circuitry to combine the ADCs to form a 14-bit, 320-MHz composite device.

Parallel Operation

Some audio circuits achieve very low noise by operating transistor amplifier stages in parallel. Theoretically, uncorrelated noise adds in an RMS fashion while the amplified signals add linearly. This means that summing the outputs from four of the same type ADCs should result in 4X the signal level but only 2X the noise. The factor of 2 (+6 dB) in the resulting SNR is equivalent to an extra bit of resolution in the combined circuit.

Of course, the ADCs run at the same sample rate they did individually, so the improvement in performance does not affect speed. Analog Devices also has a 4x parallel module, the AD10678 (now obsolete), that integrates four AD6645 14-bit, 80-MS/s ADCs, clocking, and high-speed addition/division. The ENOB of each device is specified to be 12 bits, and averaging four adds one more bit to ENOB-13 bits.⁴

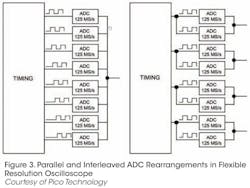
As shown in Figure 3, Pico Technology has developed the 5000 Series flexible resolution scope that trades speed for resolution over wide ranges. According to the company's press release, "In series mode, the ADCs are interleaved to provide I GS/s at 8 bits.... This mode can also provide 500 MS/s at 12 bits resolution. In parallel mode, multiple ADCs are sampled in phase on each channel to increase the resolution and dynamic performance. Resolution is increased to 14 bits at 125 MS/s per channel.... If only two channels are required, then resolution can be increased to 15 bits, and in single channel mode, all the ADCs are combined to give a 16-bit mode at 62.5 MS/s."

Signal Averaging

Signal averaging can be done in several ways. If you have a repetitive signal, averaging multiple complete acquisitions is a good way to improve resolution while causing very few unintended consequences other than slower operation. However, in general, signals are not repetitive, so acquisition averaging is of limited use.

As commented upon by Pico Technology's Tong, modern DSOS can sample at a very fast rate although they're limited to 8-bit resolution. Agilent Technologies, Tektronix, and others have used speed to advantage in their scopes that improve resolution by averaging groups of adjacent samples.

A couple of assumptions are implicit in the technique. First, there must be sufficient uncorrelated noise or additional dither present to cause random code excursions above and below the nominal code that the ADC would output for any given input level.

The assumption is that the DNL is randomly distributed throughout the ADC. As stated in an Analog Devices application note, "The main purpose of dither is to delocalize or randomize the DNL errors of the converter. In this way, the DNL of all codes appears more uniform and consistent...."⁵

Integral nonlinearity (INL) is not affected by small amounts of dither. Schemes that parallel ADCs claim to improve INL for the composite circuit because the individual INLs are not correlated. Other schemes use a high-resolution look-up table to compensate for INL errors determined in a calibration process, correcting the ADC output on-the-fly.

The second consideration is that input signals should contain frequencies only within the lowered, equivalent bandwidth of the averaging system. Boxcar averaging-so-named because of the averaging function's rectangular time-domain response-adds together N adjacent samples, divides by N, and outputs the result as the effective value of that group. The process repeats for each successive group of N samples.

Obviously, the equivalent sampling rate is reduced by a factor of N. Perhaps not so obvious is that averaging in this manner retains fast edges from the original input signal unless an anti-alias filter has suitably reduced the input bandwidth. According to Nyquist and Shannon, if a signal's frequencies all lie below half the sampling frequency—the Nyquist frequency—the original signal can be exactly reconstructed through sin(X)/X interpolation. If fast edges have been retained after boxcar averaging, reconstructing the waveform by using sin(X)/X interpolation will add Gibbs ringing.

Moving Average Smoothing

Rather than averaging successive blocks of samples, averaging can be done over the first N points, then over the N points from sample 2 to sample N+1, then from sample 3 to sample N+2, and so on. This approach has two effects. First, it shortens the acquired data record by N points. Second, it maintains the original data rate. This means that peaks appear where they should rather than possibly being offset by N (fast) sampling intervals as can happen in boxcar averaging.

A moving average is a type of FIR filter with equally weighted taps. A LeCroy application brief discussed the advantages of using a different filter tap weighting that trades slightly less improvement in noise reduction against much better frequency response characteristics.

Specifically, the LeCroy ERES FIR filter tap weighting implements a shape similar to an FFT windowing function-nearly unity in the center but tapering off toward zero at the edges.
The bell-shaped filter characteristic in the time domain has an equivalent Gaussian shape in the frequency domain. The end result is that Gibbs ringing is eliminated. The same degree of smoothing and resolution enhancement can be achieved as with a boxcar average, but the number of taps must be increased.⁶

Probes

Using a sensitive, low-noise probe is a good way to improve scope performance. Both Tek and Agilent have released higher-sensitivity current probes. As Tek's Loberg explained, "Tektronix has updated the TCP0030A to make it a safer, better performing 1-mA to 30-A current probe, with a wider jaw rated to work with uninsulated wiring safely." Also, in contrast to the low bandwidth and high loading presented by a standard 1x passive probe, the company's TPP0502 2x passive probe has a 2-MΩ, 12.7-pF input impedance with 500-MHz bandwidth.

Agilent's N2820A and N2821A AC/DC current probes measure from 50 μA to 5 A. According to the company's Kuan, "These probes work in conjunction with the new Infiniium 9000 H-Series oscilloscopes.... The higher sensitivity is especially useful for measuring current consumption of battery-powered mobile devices or integrated circuits where idle state current is often buried in the noise of the oscilloscope."

Conclusion

Agilent describes part of its sampling rate reduction/resolution improvement process as hypersampling. The term refers to boxcar 2X, 4X, 8X, or 16X averaging that's applied to the 8-bit ADC's 20-GS/s samples. In addition, the reduced rate data is further processed by a moving average filter.

Joel Woodward, senior product manager at the company's oscilloscope product division, commented on the mismatch between the 16X higher resolution the 9000H makes possible and the 3X noise reduction the scope exhibits. He said, "Oscilloscope resolution [is equal to] full screen vertical divided by the number of Q levels. So, at equal vertical scaling, an oscilloscope with 12 bits of resolution will always have 16X more resolution than an oscilloscope with 8 bits of resolution. However, resolution or bits of resolution or Q levels doesn't matter unless the noise also is considered.

"For example, at 800-mV full scale on an oscilloscope set to 100 mV/div with eight vertical divisions, noise on an oscilloscope with 8 bits of resolution might be measured at 3 mV while noise on an oscilloscope with 12 bits of resolution might be measured at 1 mV."

He concluded, "While the 12-bit scope has 16X more resolution, it only has 3X less noise. What does this mean? It means that noise will overpower and mask the LSBs, rendering some of the additional bits of resolution useless. No 500-MHz+ scope on the market today with 12 bits of resolution can utilize all of the available resolution... [because] the intrinsic noise of the scope is higher than the resolution. While today's scopes with 12 bits of resolution have lower noise than their 8-bit counterparts, scope vendors will need to [further] lower front-end noise in order to better utilize available resolution."

Noise certainly is a problem, but it's not possible to quantify how much noise is affecting high-resolution scope performance in many cases because the specifications are not listed on the datasheet. Agilent's Woodward said that the company will give ENOB information to potential buyers upon application. This may be the case with other vendors as well, which means that you need to ask if you want to find out.

As emphasized by Pico's Tong, measuring analog signals requires a different attitude than measuring digital ones. To find out how well a high-resolution scope represents a signal, you should be able to compare its dynamic performance to that of a good DAQ system.

Unfortunately, you can't do a specsheet comparison because the specifications quoted for most high-resolution scopes are incomplete. To understand how the displayed picture and related measurements compare to the actual signal, you need more detailed specifications that reflect dynamic performance. If manufacturers provided a graph of ENOB as a function of frequency, that would be a big help.

This article was originally written by Tom Lecklider and was published in Endeavor Business Media's Evaluation Engineering Magazine in July 2013

References

1. Kester, W., Understand SINAD, ENOB, SNR, THD, THD+ N. and SFDR so You Don't Get Lost in the Noise Floor, Analog Devices, MT-003 Tutorial, p. 5.

2. Evaluating High-Resolution Oscilloscopes, Agilent Technologies, Application Note 5991-1617EN, February 2013, p. 4. 

3. The Secrets Behind the MDO4000 Series Spectrum Analyzer Dynamic Range, Tektronix, White Paper, February 2013, p. 2.

4. Reeder, R., et al., Pushing the State of the Art with Multi- channel A/D Converters, Analog Dialogue, Issue 39-05, May 2005.

5. Brannon, B., Overcoming Converter Nonlinearities with Dither, Analog Devices, Application Note AN-410, December 1995, p. 5.

6. Differences Between ERES and HiRes, LeCroy, Application Brief, November 2011.