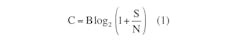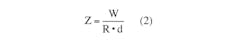A silent battle is being fought to continue making more bandwidth available to consumers, many of whom are now mobile. The ever-increasing demand for rich content and instant access to information is dividing the communications industry into two camps: one based on tried and true non-return to zero (NRZ) binary (two-level) transmission, and a newcomer called multi-level signaling (MLS).
So why leave the old standard and move to an alternative way to move digital bits? It comes down to physical limitations with our current technology. But which is more efficient for ultra-high speed communications in modern data centers, and soon the back office or your home? This is the NRZ versus MLS smack-down!
This file type includes high resolution graphics and schematics.
Background
Binary communication is as old as smoke signals. In the electrical world, it dates back to the era of Morse. Today, the computer world is essentially binary, where information based on binary principles is processed in logic. The advantage of binary is that it is extremely simple. There are only two states: 0 (zero) or off, and 1 (one) or on. This simplicity allows logical functions to be broken down into a set of switches.
Early electronic computers used tubes, and today’s modern CPUs use FINFETs. In the end, a one or a zero still determines the state. Binary communications is an extension of this concept, and information is communicated by signals sent over a medium that represents these two states.
Related Articles
- Industrial Environments Require Rugged Design
- LEDs Line Up To Replace Residential Incandescent Bulbs
- Automotive Communications Demand A Robust Infrastructure
NRZ is binary with a twist. It prevents long strings of zeros or ones in a transmission by periodically forcing or inserting a state change. The receiver knows of these insertions and removes them at the end. These insertions allow ac coupling and prevents base-line wander—or a dc shift in an electrical medium due to charging of the conductors.
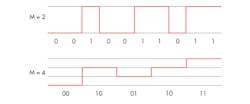
In reality, binary is a multiple-level coding scheme, one that is limited to just two levels. These two levels represent a single-bit symbol, that is, a symbol or mechanism to represent the 1 or 0. If you increase the number of bits represented by a single symbol, then theoretically you increase the capacity of the channel to carry information by compressing N-bits into M-symbols.
For example, if you encode two bits into four symbols representing 00, 01, 10, and 11, then each symbol change represents two bits—a compression of 2:1. However, this degrades the signal-to-noise-ratio (SNR) due to smaller signal level changes. The more levels, the smaller the differences between them (see the figure).
In general, it may seem that symbol-encoding the information would benefit in both the utilization of the available bandwidth and energy-per-bit used to transmit the data. But things in our physical world are not always so simple. The reality is that noise ultimately limits what is possible.
Shannon-Hartley
The Shannon-Hartley Capacity Theorem describes the theoretical limit for a given communications channel to carry information. It is based on the available bandwidth of the channel and the SNR:
Note that C represents the maximum channel capacity in bits per second, and B represents the available bandwidth. S/N represents the linear division of the average received power by the Gaussian noise interference power. By improving SNR or the bandwidth, either allows a channel to carry more information.
Given that the bandwidth is fixed, the only other two variables are received signal power and noise. By coding bits into symbols, the amount of information per state increases. But simultaneously the signal level (the difference between each symbol) decreases, causing a loss in the SNR term.
Metrics And BER
To compare the efficiencies of MLS versus NRZ, there must be a normalized method to examine how much energy is required to transport the information error free. Normalization removes the transmission speed and equalizes the comparison. A possible metric for this is shown in:
Increasing the number of bits per symbol reduces the signal level between each state, effectively reducing the SNR.
This is the energy to move one bit error free in the channel and is expressed as Joules per bit-meter. W is the total watts for both the transmitter and receiver, R is the data rate in bits per second, and d is the length of the channel in meters. The resulting metric is independent of the transmission speed and distance and allows a normalized comparison assuming similar bit error rates (BERs).
In modern communications systems, BERs are on the order of 10–12 or better. This suggests that one bit out of 1012 bits transmitted is incorrectly received. As noise and channel loss increases, this number quickly degrades and additional coding layers are required to ensure error-free transmission. All of that coding adds complexity and power.
Comparing Coding Levels
To compare MLS and NRZ, we need a standard that occupies both camps. A good candidate is Ethernet. IEEE 802.3 has several variants that incorporate both NRZ coding and multi-level. In many enterprise networks, 1000 Base-CX (short-haul copper) uses 8b/10b NRZ encoding over shielded twisted pair for a data rate of 1 Gbit/s (line rate of 1.25 Gbits/s).
There is also the ubiquitous 1000 BaseT (802.3ab) standard found in most laptops and computers today. This standard uses four pairs of category 5 (or better) bi-directionally via echo cancellation with pulse amplitude modulation or PAM-5 (5 level) encoding. The symbol rate is 125 Msymbols/s per pair, and coding is used to improve the SNR, which uses additional power.
To compare these similar technologies, let’s examine two theoretical channels: one using 1000 Base-CX, and the other using 1000 Base-T. For the first channel we’ll select a buffer/repeater required to remove loss in the channel through equalization and de-emphasis. The DS25BR100, which can run up to 3.125 Gbits/s, has a power dissipation of roughly 0.25 W for each end, for a total power of 0.5 W over 25 meters.
The DP83865 Gigabit Ethernet physical layer (PHY) consumes roughly 1.1 W for each end, for a total of 2.2 W. It can drive over 100 meters of cable (a farther reach than the DS25BR100). Using our formula to compare both standards at maximum length, we get NRZ at 2 x 10–11 J/b-m (Joules per bit-meter) and PAM-5 at 2.2 x 10–11 J/b-m.
Intuitively, the difference in efficiency should be very large, but in reality it is very close. So when the distance that the PHY can drive is considered, the differences are not as great. But in this smack-down, NRZ wins by 0.2 x 10–11 J/b-m.
Conclusion
As rates and coding levels increase beyond 10 Gbits/s, the difference between NRZ and MLS widens quickly. However, MLS may be the only way to exceed the 25-Gbit/s+ NRZ rates now being implemented by switch and infrastructure vendors. In the end, which camp will win?
There will always be a place for both since short-haul copper connections are best served by the lowest-power solutions, due to density and energy concerns. MLS may one day win the 250-Gbit/s over copper battle, but wireless and optical solutions will also be major contenders.
Reference
For more information, visit www.ti.com/comms-ca.
Richard Zarr is a technologist at Texas Instruments focused on high-speed signal and data path technology. He has more than 30 years of practical engineering experience and has published numerous papers and articles worldwide. He is a member of the IEEE and holds a BSEE from the University of South Florida as well as several patents in LED lighting and cryptography.
This file type includes high resolution graphics and schematics.