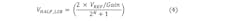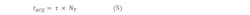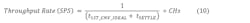Essential Timing Factors for Low-Power Precision Signal-Chain Apps (Part 1)
Members can download this article in PDF format.
What you'll learn:
- Overview of SAR vs. sigma-delta ADCs.
- Signal-chain timing considerations.
- Key ADC timing considerations.
- Digital-interface timing considerations for ADCs.
- Impact of duty cycling and integrated FIFO.
“Time is of the essence”—an old idiom that could be applied to any field. However, when applied to the sampling of real-world signals, it’s a pillar of our engineering discipline. When attempting to lower power, meet timing targets, and maintain performance requirements, consideration must be given to the type of analog-to-digital converter (ADC) architecture chosen in measurement signal chains—sigma-delta or successive approximation register (SAR).
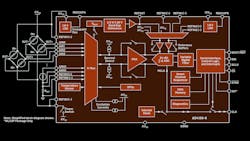
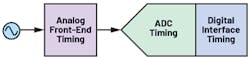
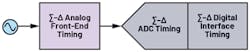
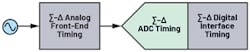
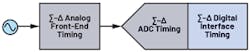
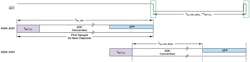
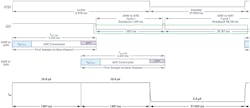
Once a particular architecture is chosen, system designers create the circuit needed to obtain the necessary system performance. At this point, designers should consider the most important timing factors for their low-power precision signal chain (Fig. 1).
1. The signal-chain timing considerations.
The Need for Speed: SAR or Sigma-Delta for Low-Power Signal Chains?
We will focus on precision low-power measurements and signals (such as temperature, pressure, and flow) with measurement bandwidths of below 10 kHz (see Precision Low Power for more details), although many of the topics covered in this article can be applied for wider bandwidth measurement systems.
When exploring low-power systems, historically, a designer would choose sigma-delta ADCs for higher-precision measurements of slow-moving signals. SARs were seen as more useful for higher-speed measurements, where more channels were converted.
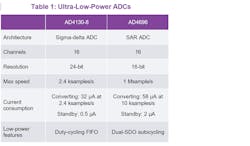
However, new SARs such as the AD4630-24 are entering the high-precision space traditionally associated with sigma-delta ADCs, so it’s not a hard and fast rule. To give real-world examples of the ADCs’ architectures, let’s look at two low-power offerings when considering the timing associated with ADC signal chain architectures: the AD4130-8 sigma-delta ADC and the AD4696 SAR ADC (Table 1).
Sample Frequency or Output Data Rate?
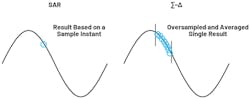
SAR converters take a sample of the input and capture the signal level at a known point in time. After the initial sample (and hold) phase, there’s a conversion phase. The time it takes to reach the result is largely based on the sampling frequency.
Sigma-delta converters take samples at a modulator frequency. The modulator oversamples, and the sample rate is much higher than the Nyquist frequency of the input signal. The additional frequency span enables the noise to be shifted to a higher frequency. The ADC then uses a process called decimation on the modulator output, where it reduces the sample rate in exchange for higher precision. It’s done through digital low-pass filters, equivalent to averaging in the time domain.
Because there’s a difference in the way that the technologies reach the conversion result, the SAR-based documentation will refer to the sample frequency (fSAMPLE) while sigma-delta datasheets will concentrate on the output data rate (ODR) (Fig. 2). We’ll guide the reader with the distinction between both as we discuss the architectures in more detail with respect to time.
2. A SAR (ƒSAMPLE) vs. sigma-delta (ODR) ADC.
With multiplexed ADCs that perform one conversion on multiple channels, the amount of time it takes to perform conversions on all channels (including setup times, etc.) is referred to as the throughput rate.
The first timing consideration for a signal chain is the time it takes to bias/excite the sensor and power up the signal chain. Voltage and current sources will have to turn on, with sensors biased and startup time specifications considered. The turn-on settling time for the AD4130-8 on-chip reference is 280 µs for a specific load capacitance on the reference pin, for example. The on-chip bias voltage, which can be used to excite sensors, has an associated startup time of 3.7 µs per nF, but this depends on the amount of capacitance attached to the analog input pins.
Signal-Chain Timing Considerations When Using Sigma-Delta ADCs
After power-up times in the signal chain are investigated, we need to look at timing considerations that apply depending on the ADC architecture. The next section of the article concentrates on measurement signal chains that have sigma-delta ADC at their core when used in an ultra-low-power applications and the important timing considerations associated with this type of ADC.
There will be some overlap between SAR and sigma-delta signal chains that impact timing, such as using techniques that look at minimizing the microcontroller interaction time to achieve system-level power-consumption improvements. These will be highlighted when we move onto the SAR ADC signal chains.
If the ADC of choice is sigma-delta as opposed to a SAR, there will be a particular set of timing considerations that need to be considered. The principal areas to explore when looking at a signal chain are the analog front-end timing, ADC timing, and the digital interface timing (Fig. 1, again).
Analog Front-End Timing Considerations
We’ll focus on the three blocks independently, starting with the analog front end (AFE) (Fig. 3). The AFE can vary depending on the type of design, but some common aspects can apply to most circuits.
3. The analog-front-end sigma-delta timing considerations.
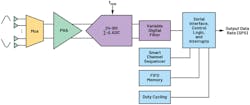
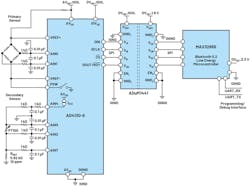
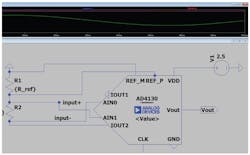
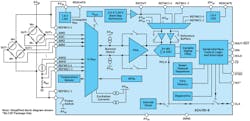
The AD4130-8, part of Analog Devices’ precision low power group of signal chain products (mentioned above), is the lowest-power sigma-delta ADC. It’s specifically designed with rich features set to reduce power while still achieving a high level of performance. Some of these features include an on-board FIFO, a smart channel sequencer, and duty cycling (Fig. 4). It contains many key signal-chain building blocks on-chip, such as a voltage reference, programmable gain amplifier (PGA), multiplexer, and sensor excitation current or sensor bias voltage, and yet maintains an ultra-low current.
4. The AD4130 sigma-delta simplified system blocks.
When we consider the AFE of this device, it consists of an on-chip PGA that minimizes the analog input current, which removes the need for external amplifiers to drive the inputs. Oversampling followed by a digital filter ensures that the bandwidth is dominated by the digital filter.
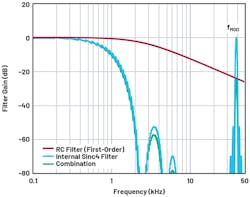
The AD4130-8 incorporates a number of sinc3 and sinc4 filters as well as filters designed to reject 50- and 60-Hz noise. The sinc3 and sinc4 digital filters require a supplementary external antialiasing filter. The purpose of this antialiasing filter is to limit the amount of bandwidth of the input signal. This is to ensure that noise, for example, with a rate of change at fMOD (the modulator frequency) doesn’t alias into the passband and into the conversion result (Fig. 5).
5. A simulation of combined external and internal filtering.
Antialiasing Filter
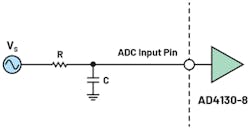
Higher-order antialiasing filters can be used, but designers typically turn to first-order, single-pole, low-pass filters to satisfy requirements (Fig. 6).
6. A first-order low-pass antialiasing filter.
Filters are designed based on sampling the signal of interest, with Equation 1 dictating the filter 3-dB BW:
When selecting the capacitor values and resistance values, a higher resistance is more desirable but may increase noise. On the other hand, the lower capacitor values reach a limit after which the ratio of the pin capacitance to the external capacitance becomes relevant.
It’s important to know the time it will take the circuit to charge based on the maximum voltage step that could be seen across this capacitor.
The voltage seen at the capacitor will change with respect to time at rate of change of:
where VC = voltage across the capacitor at a point in time; VS = supply voltage applied; and t = time.
On power-up, VS, the step size could be equal to the full input voltage range of the ADC (±VREF/gain).
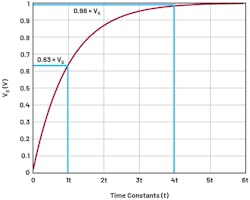
Figure 7 shows that after four time constants (𝜏 = R × C), the signal has reached 0.98 × VS.
7. First-order low-pass filter settling time in response to a 1-V full-scale step change.
The number of time constants required can be calculated from the natural logarithm of the ratio of the step size, VS:
NT is the number of time constants to wait for, if the input is to settle to within half of an LSB (VHALF_LSB) of the ADCs’ input voltage span. The VHALF_LSB in the previous formula can be substituted based on the required voltage accuracy. If the system designer wishes to resolve to within half an LSB, for a bipolar input ADC with N bits of resolution and with internal PGA gain = 1, this will be:
The time that it takes to resolve to the real input volage tACQ becomes the number of time constants multiplied by t, which is equal to RC:
Traditionally, when switching between channels on multiplexed ADCs, a large voltage swing (one channel at negative full scale, the next channel at positive full scale) between channels would require the similar calculation. The AD4130-8 solves this problem by implementing a low-power on-chip precharge buffer that turns on when switching between channels. This ensures that at the fastest data rates, the first conversion after switching channels will be converted correctly.
There’s also an on-chip PGA designed to allow for a full common-mode input range, giving system designers a greater margin for widely varying common-mode voltages. This is useful for measuring signals, but in the worst case, one channel could be at negative full scale while the next channel could be at positive full scale.
Example: Analog Front-End Low-Pass Filter
The example in Figure 8 shows a Wheatstone bridge sensor with a –3 dB filtering for a 24-bit ADC just below 16 kHz: R = 1 kΩ, C = 0.01 µF with VREF = 2.5 V and the PGA gain set to 1.
8. An isolated AD4130-8 circuit with a low-pass filter is shown.
The single-ended filters in Figure 8 show the primary sensor R = 1 kΩ and C = 0.01 µF:
As the differential sensor time constant dominates the single-ended values, it will dictate the overall system calculation:
This is the time a system designer would need to enable the filter to settle externally before gathering a sample on power-up. This can be done in the digital domain by discarding samples or the sample instant can be delayed to account for this charging.
When designing a filter, the resistor and capacitor values may be different to what’s shown earlier. System designers can model the filter together with the AD4130-8 using LTspice. LTspice also can be used to model a system or signal chains as shown in Figure 9, where we’re simulating an RTD behavior by varying R2.
9. A simulation of an RTD (R2) circuit in LTspice.
ADC Timing Considerations
Recalling that output data rates are how we refer to sigma-delta ADCs’ timing, let’s examine the internal timing associated with this type of ADC (Fig. 10).
10. The sigma-delta ADC timing considerations.
This type of converter digitizes an analog signal with a low-resolution (1 bit) ADC at a high sampling rate. Using oversampling techniques in conjunction with noise shaping and digital filtering increases the effective resolution.
An SPI write to a digital register lets users control the oversampling and decimation rate of the AD4130-8. The modulator sample rate (fMOD) is fixed. The FS value essentially changes the number of samples (in increments of 16 for the AD4130-8) used by the digital filter to reach a result. Varying the FS word changes the number of oversampled modulations clocks per ADC result.
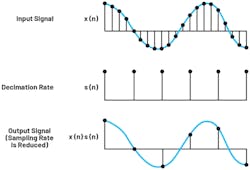
As decimation reduces the effective sampling rate at the ADC output, it achieves higher accuracy (Fig. 11). Decimation can be viewed as the method that removes the redundant signal information introduced by the oversampling process.
11. As decimation reduces the effective sampling rate at the ADC output, it achieves higher accuracy.
The more decimation that’s used (the more samples included in the digital filter calculation), the more accuracy is achieved by the said digital filter, but the slower the output data rate:
where fADC is the output data rate; fMOD is the master clock frequency; and FS is the multiplier used to control the decimation ratio.
Filter Latency
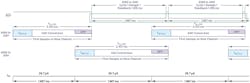
When more than one channel is enabled, the link between the datasheet ODR (fADC) and the data throughput rate is more complex. This is due to the latency of the digital filter when switching channels. The time needed for the digital filters to settle depends on the sinc filter type.
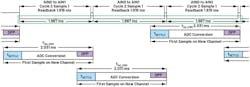
Figure 12 shows that the first conversion of a sinc3 filter will take three conversion cycles until the digital equivalent to the analog input is reached. The first conversion of a sinc4 filter will take four conversion cycles. The tSETTLE is the user-programmable settle time that considers the multiplexer switching. The higher the filter order, the lower the noise, but the downside is the number of conversion cycles needed for the filter to settle.
12. Shown is an example of filter latency.
Digital-Interface Timing Considerations
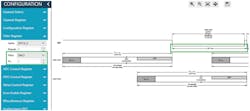
To aid in the understanding of the digital-interface timing in sigma-delta ADCs like the AD4130 (Fig. 13), a model is available via Analog Devices’ software tool, ACE. The timing tools are part of several software tools integrated into the ACE software. Included are a sequencer timing diagram and a FIFO timing diagram to aid in the understanding of these configurations.
13. AFE sigma-delta digital-interface timing considerations.
The AD4130-8 sequencer allows different input channels to have different digital filter and settling configurations and timing. The timing tool simplifies the process of calculating when data will be available to read.
When more than one channel is enabled, the user should not make the mistake of reading a settled channel ODR and dividing by the number of channels enabled to calculate the throughput rate. That’s because it doesn’t consider digital filter latency. The filter latency should be taken into account when calculating the throughput rate (effective ODR vs. datasheet ODR). When more than one channel is enabled, the initial settling (tSETTLE) needs to be calculated, as well as the number of internal conversion cycles (t1st_CONV_IDEAL), as shown in Figure 14.
14. The first conversion output data rate including filter latency.
If all channels have the same filter plus settling configuration and there are no repeat conversions on any channels, the throughput rate of a system becomes:
where CHs = is the number of channels enabled; t1ST_CNV_IDEAL = is the conversion time including the filter latency; and tSETTLE = a digitally controlled timing parameter that can be extended but with a minimum programmable time to account for the multiplexer settling.
The throughput rate can be calculated by looking at the sum of the 1CNV_ODR times, which is the time shown between the green squares in Figure 14:
Example: Pressure-Sensor Signal-Chain Timing
If we want to design a system with multiple pressure sensors, represented by the pressure sensors in Figure 15, accompanied by a temperature sensor:
- Question A: How many pressure sensors per AD4130-8 can be deployed in the system?
- Question B: What resolution can we expect if the voltage output range from the pressure sensor is 3 mV/V?
- Question C: If a line in the plant needs at least 14 bits of effective resolution to meet the dynamic range system demands, how many load cells form the system?
15. A simplified pressure-sensor system block diagram.
Part A
Step 1: Choose the gain.
- AVDD = 1.8 V. REFIN+ to REFIN– = 1.8 V
- The 1.8-V excitation of the load cell at 3 mV/V will lead to a 5.4 mV maximum output of each load cell.
- The maximum gain on the PGA = 128.
- The ADC input will see 5.4 mV × 128 = 0.7 V across its inputs, well within the 1.8-V range. A PGA gain of 128 is the correct gain to use.
Step 2: Choose the FS value.
We want to choose the fastest settings that are with a sinc3 filter and FS = 1.
Step 3: Use the throughput rate for one channel to calculate the number of channels in the system (Fig. 16).
16. Calculating the sum of t1CNV_ODR using the timing tool.
- 1CNV_ODR = (1/1.667 ms) 600 samples/s.
- Throughput rate = 600 samples/s/Nch.
- 1CNV_ODR = Throughput rate for a single channel in a multichannel system with the same configurations and no repeat conversions.
- 10 channels can be sampled at 60 samples/s.
Answer A: Nine load cells per system.
Step 4: Use the datasheet effective resolution tables.
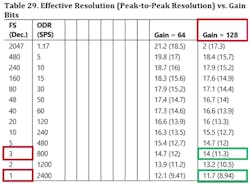
Another point to consider is that when looking at noise and effective resolution tables, the calculations need to be based on the FS filter value and not the throughput rate. The ODR listed here is the settled channel ODR on a single channel (Fig. 17).
17. FS word vs. gain.
System designers need to be careful when interpreting the datasheet. When more than one channel is enabled, the throughput rate in samples per second decreases. There’s a danger that readers might incorrectly interpret the resolution tables in the data sheet and think that a higher resolution is achievable.
With settled channel ODR, the change in FS leads to an increase of oversampling and decimation that slows down the system to achieve higher accuracy. In the case when more than one channel is enabled, the decrease in speed of reading from each ADC channel in samples per second (throughput) is due to sampling on more than one channel. It’s not caused by an increase in oversampling; hence, there’s no increase in the resolution.
Part B
If we look at the table in the datasheet, we see that the effective resolution is 11.7 bits for FS = 1 and gain = 128 (Fig. 18).
Answer B: 11.7 bits.
18. A resolution vs. gain datasheet table.
Part C
To solve for C, we need to return to a couple steps from Part A:
Step 2: Choose the FS value.
This time, we choose the FS value based on the resolution requirement. To achieve an effective resolution of 14 bits, an FS of 3 should be chosen.
Step 3: Use the throughput rate for one channel to calculate the number of channels in the system (Fig. 19).
- We can use the timing AFM to achieve the resolution needed (1/4.167 μs).
- 240 samples/s/Nch = Throughput rate.
- We can use four channels at this data rate.
Answer C: Three channels.
19. The timing tool is used to change the filter type and FS value and read the output data rate of the first conversion that includes filter latency.
Duty Cycling
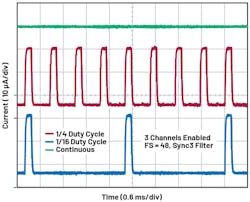
There are systems with lower throughput rates and higher output data rates, such as health-monitoring devices where the host controller would put the system in standby mode most of the time and convert periodically. Duty cycling, available on the AD4130-8, allows the user to continuously convert with the part entering standby mode for 3/4 or 15/16 of the duty cycle, while the part converts for 1/4 or 1/16 of the duty cycle (Fig. 20). Active time and standby time are functions of the settings chosen by the user.
20. Shown is an example of duty cycling.
The AD4130-8 also incorporates a SYNC pin that lets the user deterministically control when conversions take place on a preselected number of channels. In addition, the part can be configured to work in a reduced current standby mode, initiate a conversion sequence, leave the reduced current state, convert on a number of channels, and return to standby mode when the conversions are completed.
Example: Enabling Duty Cycling
Taking the same settings as the previous pressure-sensor signal-chain example and the throughput rate = 600 samples/s/Nch, enabling two channels, the ODR becomes 300 samples/s while the average current would be 28.7 µA on average with a 3-V supply (Fig. 21).
21. The throughput time and current before enabling duty cycling.
After enabling duty cycling 1/16, the throughput rate becomes 24.489 samples/s while the average current becomes 4.088 µA over that period (40.834 ms) (Fig. 22).
22. The throughput time and current after enabling duty cycling.
FIFO
The AD4130-8 includes an on-board FIFO. A FIFO reduces system power by buffering the conversions and providing the opportunity for a microcontroller or host controller to enter a low-power state while waiting for conversions. The biggest timing consideration here is to ensure the host reads back the FIFO quickly enough while continuously converting to avoid missed conversions.
The user can periodically read the FIFO when a specified number of samples (also known as watermark) has been gathered. When a desired number of samples is reached, an interrupt is available, and the host reads back the FIFO. The FIFO must be emptied to clear the interrupt. The user has a predefined period of time to read back data from the FIFO. The SCLK frequency used will determine how much data one can read without missing conversions.
With the ACE software timing tool, the user can vary the SCLK frequency or use a gated clock to inform when the watermark level needs to be reduced while designing the system (Fig. 23). One such example is the FIFO readback.
23. The AD4130-8 ACE software FIFO readback window and alert.
For instance, take a continuous single-channel measurement running at the maximum ODR of 2400 ksamples/s. If the watermark level is set to 256 and we attempt to read back, we have 729.2 µs to read back the FIFO without missing a conversion. The user needs to read back 4112 bits.
The tool informs the user that in order to read the FIFO back and not miss a conversion, 5.64 MHz of a host SPI clock frequency is needed. This breaks the 5-MHz maximum specification for the part and an error appears, allowing the user to modify the watermark to avoid breaking specification.
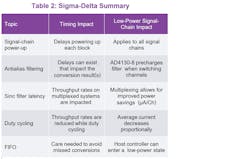
When a sigma-delta ADC is used, we can see that there are plenty of trade-offs, timing factors, and features to consider (Table 2). Part 2 of this article will examine the SAR ADC technology as well as the factors and features that impact timing in SAR ADC-based systems.
References
Maithil Pachchigar. “Design Trade-Offs of Using Precision SAR and Sigma-Delta Converters for Multiplexed Data Acquisition Systems.” Analog Devices, Inc., April 2016.
Walt Kester. “Which ADC Architecture Is Right for Your Application?” Analog Dialogue, Vol. 39, No. 9, June 2005.
Albert O’Grady. “Transducer/Sensor Excitation and Measurement Techniques.” Analog Dialogue, Vol. 34, No. 5, 2000.
Alan Walsh. “Front-End Amplifier and RC Filter Design for a Precision SAR Analog-to-Digital Converter.” Analog Dialogue, Vol. 46, No. 12, December 2012.
Steven Xie. “Practical Filter Design Challenges and Considerations for Precision ADCs.” Analog Dialogue, Vol. 50, No. 4, April 2016.
Walt Kester. “MT-021: ADC Architectures II: Successive Approximation ADCs.” Analog Devices, Inc., 2009.
Ke Li and Colm Slattery. “Electromagnetic Flow Meters: Design Considerations.” Analog Dialogue, Vol. 50, No. 6, June 2016.
“SPICE Model for a Platinum RTD Sensor.” Analog Devices, Inc., 2022.
“MT-070 Tutorial: In-Amp Input RFI Protection.” Analog Devices, Inc., 2009.